Score : $1400$ points

Problem Statement

In the country there are $N$ cities numbered $1$ through $N$, which are connected by $N-1$ bidirectional roads. In terms of graph theory, there is a unique simple path connecting every pair of cities. That is, the $N$ cities form a tree. Besides, if we view city $1$ as the root of this tree, the tree will be a full binary tree (a tree is a full binary tree if and only if every non-leaf vertex in the tree has exactly two children). Roads are numbered $1$ through $N-1$. The $i$-th road connects city $i+1$ and city $a_i$. When you pass through road $i$, the toll you should pay is $v_i$ (if $v_i$ is $0$, it indicates the road does not require a toll).

A company in city $1$ will give each employee a family travel and cover a large part of the tolls incurred. Each employee can design the travel by themselves. That is, which cities he/she wants to visit in each day and which city to stay at each night. However, there are some constraints. More details are as follows:

• The travel must start and end at city $1$. If there are $m$ leaves in the tree formed by the cities, then the number of days in the travel must be $m+1$. At the end of each day, except for the last day, the employee must stay at some hotel in a leaf city. During the whole travel, the employee must stay at all leaf cities exactly once.
• During the whole travel, all roads of the country must be passed through exactly twice.
• The amount that the employee must pay for tolls by him/herself is the maximum total toll incurred in a single day during the travel, except the first day and the last day. The remaining tolls will be covered by the company.

Shik, as an employee of this company, has only one hope for his travel. He hopes that the amount he must pay for tolls by himself will be as small as possible. Please help Shik to design the travel which satisfies his hope.

Constraints

• $2 < N < 131,072$
• $1 \leq a_i \leq i$ for all $i$
• $0 \leq v_i \leq 131,072$
• $v_i$ is an integer
• The given tree is a full binary tree

Input

The input is given from Standard Input in the following format:

$N$

$a_1$ $v_1$

$a_2$ $v_2$

$:$

$a_{N-1}$ $v_{N-1}$

Output

Print an integer denoting the minimum amount Shik must pay by himself for tolls incurred during the travel.

7
1 1
1 1
2 1
2 1
3 1
3 1

4

There are $4$ leaves in the tree formed by the cities (cities $4$, $5$, $6$, and $7$), so the travel must be $5$ days long. There are $4! = 24$ possible arrangements of the leaf cities to stay during the travel, but some of them are invalid. For example, $(4,5,6,7)$ and $(6,7,5,4)$ are valid orders, but $(5,6,7,4)$ is invalid because the route passes $4$ times through the road connecting city $1$ and city $2$. The figure below shows the routes of the travel for these arrangements.

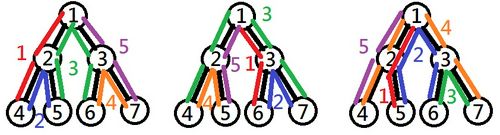
For all valid orders, day $3$ is the day with the maximum total incurred toll of $4$, passing through $4$ roads.

9
1 2
1 2
3 2
3 2
5 2
5 2
7 2
7 2

6

The following figure shows the route of the travel for one possible arrangement of the stayed cities for the solution. Note that the tolls incurred in the first day and the last day are always covered by the company.

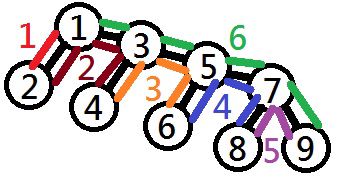
15
1 2
1 5
3 3
4 3
4 3
6 5
5 4
5 3
6 3
3 2
11 5
11 3
13 2
13 1

15

3
1 0
1 0

0