atcoder#AGC007E. [AGC007E] Shik and Travel
[AGC007E] Shik and Travel
配点 : 点
問題文
ある国には 個の都市があり、それらは 本の道路で結ばれています。道路は双方向に通行できます。便宜上、都市には から の、道路には から の番号が振られています。グラフ理論の用語を用いると、任意の二つの都市に対し、それらを結ぶ単純道がちょうど一つ存在します。すなわち、都市と道路から構成されるグラフは木です。また、 番の都市をこの木の根とみなすと、この木は全二分木となっています。(全二分木とは、葉以外の任意の頂点がちょうど二つの子を持つような根付き木のことをいいます。) 番の道路は 番の都市と 番の都市を結び、一回の通行ごとに の通行料が発生します。( が であるような道路では通行料は発生しません。)
番の都市に、社員の旅行を奨励していることで有名な会社があります。この会社には道路通行料補助制度という制度があり、社員の旅行中に発生する道路の通行料のほとんどを会社が負担します。旅行がこの制度の適用対象となるためにはいくつかの制約を満たす必要があり、その範囲内であれば好きなように旅程を決めることができます。これらの詳細は以下の通りです。
- 制度の適用対象となるためには、旅行の出発点と終着点はともに 番の都市でなければならない。また、この国の都市と道路を 番の都市を根とする根付き木とみなしたとき、この木の葉の個数を とすると、旅行日程は 泊 日でなければならない。これらの 回の宿泊は、木の葉に相当する都市のすべてで一度ずつ行わなければならない。
- 旅行全体を通じて、この国のすべての道路をそれぞれちょうど二度ずつ通行しなければならない。
- 旅行中に発生する道路の通行料のうち、社員自身が負担しなければならない金額は、発生する通行料の合計が最大であるような日(ただし旅行初日および最終日を除く)に発生する通行料の合計である。残りの金額は会社の負担となる。
シックはこの会社の従業員です。道路通行料補助制度のもとで行う今度の旅行では、発生する通行料のうち自分自身で支払わなければならない金額を最小にすることだけを考えています。そのような旅程を組む手伝いをしてあげてください。
制約
- すべての に対し、
- は整数である。
- 与えられる木は全二分木である。
入力
入力は以下の形式で標準入力から与えられる。
出力
道路通行料補助制度のもとで旅行を行うとき、発生する通行料のうち自分自身で負担しなければならない金額の最小値を出力せよ。
7
1 1
1 1
2 1
2 1
3 1
3 1
4
都市と道路を 番の都市を根とする根付き木とみなしたとき、この木には 個の葉が存在するため( 番の都市に相当する頂点)、 旅行日程は 泊 日となります。これらの つの都市に宿泊する順序は 通り存在しますが、そのうちの一部では道路通行料補助制度の対象外となってしまいます。例えば、 や の順に都市を訪れると制度の対象になりますが、 の順に訪れると経路中に 番の都市と 番の都市を結ぶ道路を 回通ってしまい、制度の対象外となってしまいます。下図にこれらの訪問順序に対応する旅行の経路を示します。
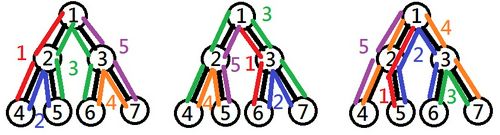
制度の対象となるような都市の訪問順序すべてにおいて、対応する旅程では 日目に 本の道路を通行して合計で の通行料が発生し、発生する通行料の合計が最大であるような日はこの日となります。
9
1 2
1 2
3 2
3 2
5 2
5 2
7 2
7 2
6
下図に負担金額が最小となるような旅行の経路をひとつ示します。
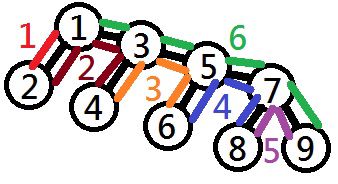
負担金額を算出する際に、旅行初日および最終日に発生する通行料は考えないことに注意してください。
15
1 2
1 5
3 3
4 3
4 3
6 5
5 4
5 3
6 3
3 2
11 5
11 3
13 2
13 1
15
3
1 0
1 0
0
