1 条题解
-
1
好像题解里没有倍增的?来一发(逃。
前置芝士:
倍增,基数排序。
倍增求 SA:
首先,朴素思路大家肯定都知道,就是从最后一位开始枚举,然后每次存下当前枚举到的字符串,最后排序并输出就 OK 辣!
但是时间复杂度是我们接受不了的,枚举字符串 ,排序 ,所以倍增的思路就是每次枚举长度(当然是从 )。
所以我们的排序画成图的是这样的(下文称字符串为 ):
第一次就相当于是按每个后缀的首字母排序。

第二次向后了一位,因为已经根据首字母拍了一次序,所以现在就根据后面的排序,类似于第一关键字,第二关键字。
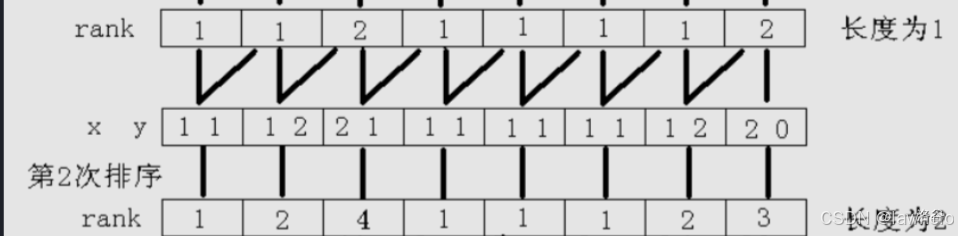
好,第三次,向后扩展了两位,不就是上一次的排序结果加上最后一位(就是第一次的)排序结果吗?所以也是轻松得到。
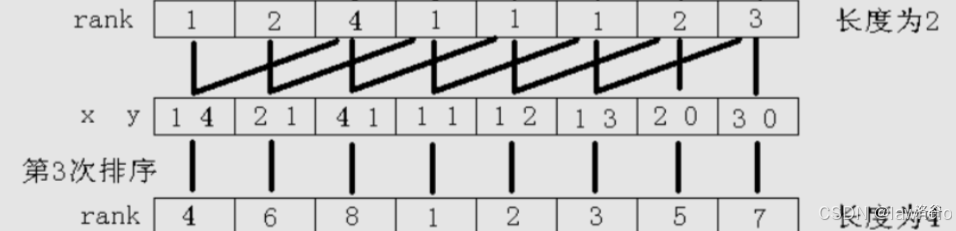
第四次,扩展了四位,欸,好像向后扩展的都在之前被更新过了,所以直接就可以用之前的结果和当前的 的排名把现在的更新就好了,大概是 的。
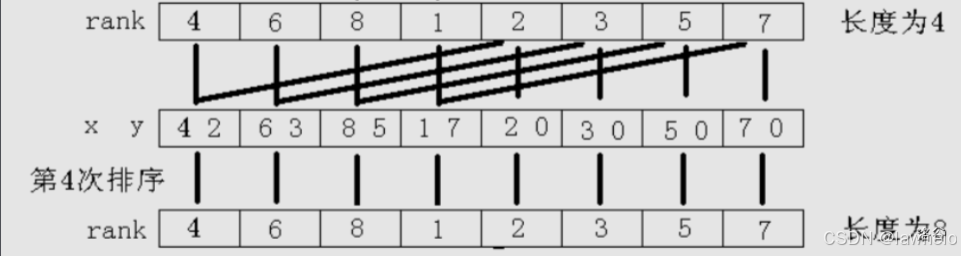 注:这里我们每次都会借助更新后的 数组辅助排序,避免每次重新暴力排,所以每次相当于是上一次的排序结果加上这一次的排序结果。
注:这里我们每次都会借助更新后的 数组辅助排序,避免每次重新暴力排,所以每次相当于是上一次的排序结果加上这一次的排序结果。但本题还要我们求出 数组,这时候直接利用 数组以及他的 数组求就好了(逃。
code:
# include <bits/stdc++.h> # define rank chtolly using namespace std; int sa[300011], t1[300011], t2[300011], c[300011], n, rank[300011], heigh[300011]; char s[300011]; void build (int m = 300) { int *x = t1, *y = t2; for (int i = 1; i <= m; i ++) c[i] = 0; for (int i = 1; i <= n; i ++) c[x[i] = s[i]] ++; for (int i = 1; i <= m; i ++) c[i] += c[i - 1]; for (int i = n; i >= 1; i --) sa[c[x[i]] --] = i; for (int j = 1; j <= n; j <<= 1) { int p = 0; for (int i = n - j + 1; i <= n; i ++) y[++ p] = i; for (int i = 1; i <= n; i ++) if (sa[i] > j) y[++ p] = sa[i] - j; for (int i = 1; i <= m; i ++) c[i] = 0; for (int i = 1; i <= n; i ++) c[x[y[i]]] ++; for (int i = 1; i <= m; i ++) c[i] += c[i - 1]; for (int i = n; i >= 1; i --) sa[c[x[y[i]]]-- ] = y[i]; swap (x, y); p = 1; x[sa[1]] = 1; for (int i = 2; i <= n; i ++) { x[sa[i]] = y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + j] == y[sa[i] + j] ? p : ++ p; } if (p >= n) break; m = p; } } void make () { int k = 0; for (int i = 1; i <= n; i ++) rank[sa[i]] = i; for (int i = 1; i <= n; i ++) { if (rank[i] == 1) continue; if (k) k --; int j = sa[rank[i] - 1]; while (j + k <= n and i + k <= n and s[i + k] == s[j + k]) { ++ k; } heigh[rank[i]] = k; } } int main () { scanf ("%s", s + 1); n = strlen (s + 1); build (); for (int i = 1; i <= n; i ++) printf ("%d ", sa[i] - 1); puts (""); make (); for (int i = 1; i <= n; i ++) printf ("%d ", heigh[i]); puts (""); }
- 1
信息
- ID
- 7837
- 时间
- 2000ms
- 内存
- 256MiB
- 难度
- 6
- 标签
- 递交数
- 22
- 已通过
- 12
- 上传者
