题目描述

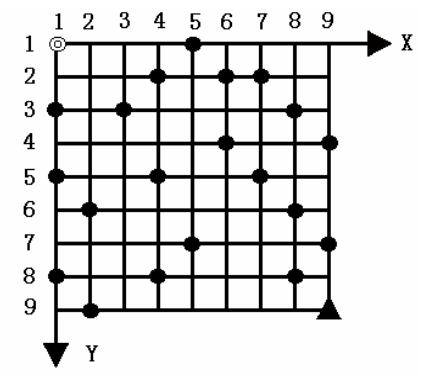
给定一个 $\text{N}\times \text{N}$ 的方形网格，设其左上角为起点◎，坐标为 $\text{(1,1)}$ ，$\text{X}$ 轴向右为正， $\text{Y}$ 轴向下为正，每个方格边长为 1 ，如图所示。

一辆汽车从起点◎出发驶向右下角终点▲，其坐标为 $(\text{N},\text{N})$ 。

在若干个网格交叉点处，设置了油库，可供汽车在行驶途中加油。汽车在行驶过程中应遵守如下规则:

• 汽车只能沿网格边行驶，装满油后能行驶 $\text{K}$ 条网格边。出发时汽车已装满油，在起 点与终点处不设油库。

• 汽车经过一条网格边时，若其 $\text{X}$ 坐标或 $\text{Y}$ 坐标减小，则应付费用 $\text{B}$ ，否则免付费用。

• 汽车在行驶过程中遇油库则应加满油并付加油费用 $\text{A}$。

• 在需要时可在网格点处增设油库，并付增设油库费用 $\text{C}$ (不含加油费用 $\text{A}$ )。

• $N , K , A , B , C$ 均为正整数， 且满足约束: $2\leq \text{N} \leq 100, 2 \leq \text{K} \leq 10$。

设计一个算法，求出汽车从起点出发到达终点的一条所付费用最少的行驶路线。

输入格式

文件的第一行是 $\text{N,K,A,B,C}$ 的值。

第二行起是一个$\text{N}*\text{N}$ 的 0-1 方阵,每行 $N$ 个值,至 $\text{N}+1$ 行结束。

方阵的第 $\text{i}$ 行第 $\text{j}$ 列处的值为 1 表示在网格交叉点 $(\text{i},\text{j})$ 处设置了一个油库,为 0 时表示未设油库。各行相邻两个数以空格分隔。

输出格式

程序运行结束时,输出最小费用。

9 3 2 3 6
0 0 0 0 1 0 0 0 0
0 0 0 1 0 1 1 0 0
1 0 1 0 0 0 0 1 0
0 0 0 0 0 1 0 0 1
1 0 0 1 0 0 1 0 0
0 1 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0 1
1 0 0 1 0 0 0 1 0
0 1 0 0 0 0 0 0 0

12

数据范围与提示

$2\leq n\leq 100$

$2 \leq k \leq 10$