题目描述

译自 ROI 2016 Day1 T4. Обитаемые горы

基于斯特鲁伽茨基兄弟的小说《人烟之岛》。 译者没时间翻译完整题面了，泥萌先甭看故事了

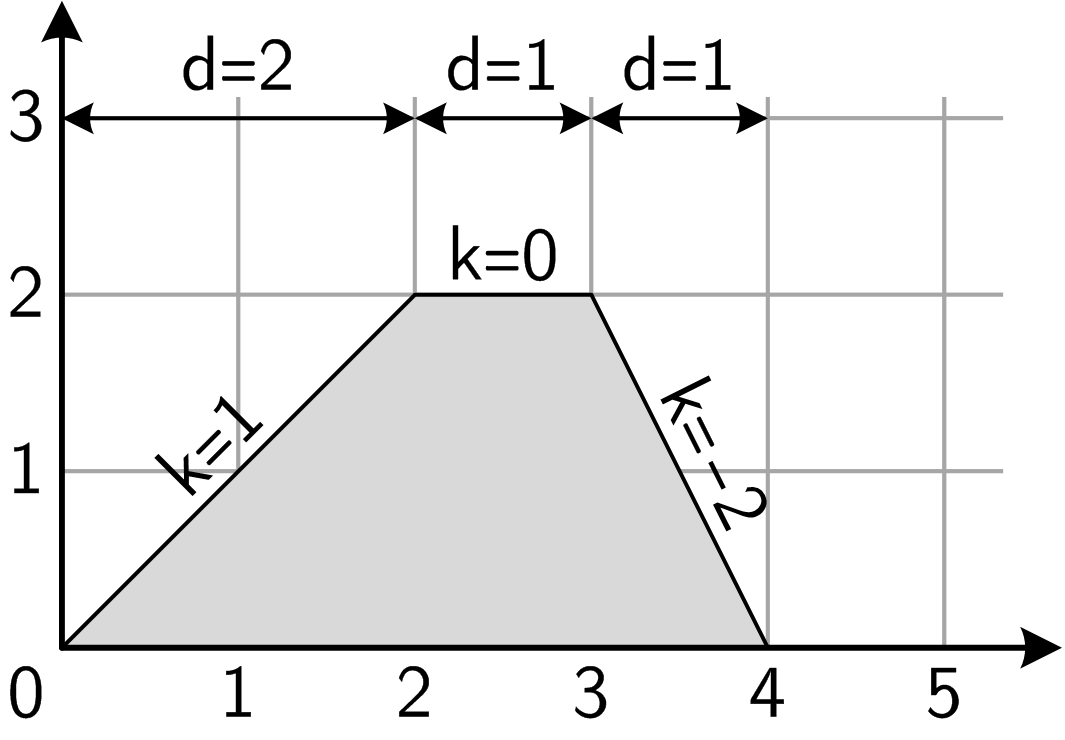
某地地形可用 $n$ 段折线来表示（下文称之为多段线），这 $n$ 段折线连接了 $n+1$ 个拐点，且保证没有垂直线。我们将拐点从左到右依次编为 $0\ldots n$ 号。我们将最左侧的点（即 $0$ 号点）设为原点，然后给出每一段的射影长度（即该线段的两个端点的横坐标之差）和斜率。保证 $n$ 号点的纵坐标为 $0.$

在某些位置将建起瞭望塔，瞭望塔上有一个或一些瞭望台。假设已知点 $A$ 和点 $B$，如果线段 $AB$ 上没有点严格位于多段线以下，那么我们称点 $A$ 可以看到点 $B$。

该地共有 $q$ 个瞭望台。给出所有瞭望台的位置。对于 $j=1\ldots q,$ 试求：从 $j$ 号瞭望台的塔基向左 / 右走，一直走到什么地方时还能看到该瞭望台，而再走远一点点就看不到了。（我们称之为该瞭望台的视界。）

输入格式

第一行有两个整数 $n,q$。
第二行有一个整数 $C,$ 保证 $C=10^4$ 或 $10^9$。这个数会提示下面输入的数据的范围。
接下来 $n$ 行，每行两个整数 $d_i,$ $k_i$ $(1 ⩽ d_i ⩽ C,$ $−C ⩽ k_i ⩽ C)$。
接下来 $q$ 行，每行两个整数 $u_j,$ $v_j$ $(0 ⩽ u_j ⩽ C,$ $−C ⩽ v_j ⩽ C),$ 表示瞭望台的坐标。

输出格式

共 $q$ 行，每行两个整数，表示该瞭望台的视界。

6 1
3 1
2 -1
1 1
1 -1
1 1
2 -1
5 3

3 8

5 3
1 1
1 -2
2 0
2 1
1 -1
3 0
3 5
3 3

1 6
0 7
0 6

6 4
1 2
2 -2
1 1
1 -2
4 1
1 -1
1 4
3 4
10 4
7 4

0 4
1 9
4 10
1 10

8 4
1 -3
2 0
1 1
2 0
1 -3
1 3
1 2
1 0
2 -2
6 -1
6 4
7 -4

0 6
4 9
0 10
6 9

数据范围与提示