atcoder#ASAPORO2B. Many Swaps Sorting
Many Swaps Sorting
题目描述
すぬけくんは を並び替えて得られるような数列 を持っています。 の (-indexedでの) 番目の数は です。
すぬけくんは の番号がついた 種類の操作を自由な順番で何度でも行うことができます。 番の操作を行うと以下のソースコードで表されるような処理が実行されます。
for(int i=k;i<N;i++)
swap(p[i],p[i-k]);
すぬけくんは操作を 回以上 回以下行って を昇順に並び替えたいです。そのような操作手順の一例を示してください。 なお、この問題の制約下で、そのような操作手順が必ず存在することが証明できます。
输入格式
入力は以下の形式で標準入力から与えられる。
输出格式
操作回数(これを とする)を 行目に出力せよ。 続く 行のうち 行目には 番目に実行する操作の番号を出力せよ。 が 以下であり、 回の操作後に が昇順となっていれば正解となる。
5
4 2 0 1 3
4
2
3
1
2
9
1 0 4 3 5 6 2 8 7
11
3
6
1
3
5
2
4
7
8
6
3
提示
制約
- は を並び替えて得られる
部分点
- 点分のデータセットでは が成立する
- 別の 点分のデータセットでは が成立する
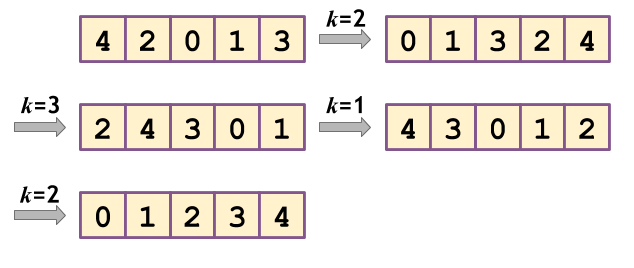
Sample Explanation 1
- 以下の図に各操作による の変化を示します。