Score : $700$ points

Problem Statement

You are given $N$ points $(x_i,y_i)$ located on a two-dimensional plane. Consider a subset $S$ of the $N$ points that forms a convex polygon. Here, we say a set of points $S$ forms a convex polygon when there exists a convex polygon with a positive area that has the same set of vertices as $S$. All the interior angles of the polygon must be strictly less than $180^\circ$.

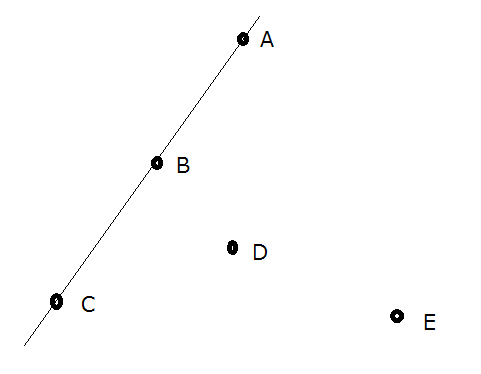
For example, in the figure above, {$A,C,E$} and {$B,D,E$} form convex polygons; {$A,C,D,E$}, {$A,B,C,E$}, {$A,B,C$}, {$D,E$} and {} do not.

For a given set $S$, let $n$ be the number of the points among the $N$ points that are inside the convex hull of $S$ (including the boundary and vertices). Then, we will define the score of $S$ as $2^{n-|S|}$.

Compute the scores of all possible sets $S$ that form convex polygons, and find the sum of all those scores.

However, since the sum can be extremely large, print the sum modulo $998244353$.

Constraints

• $1 \leq N \leq 200$
• $0 \leq x_i,y_i<10^4 (1 \leq i \leq N)$
• If $i \neq j$, $x_i \neq x_j$ or $y_i \neq y_j$.
• $x_i$ and $y_i$ are integers.

Input

The input is given from Standard Input in the following format:

$N$

$x_1$ $y_1$

$x_2$ $y_2$

$:$

$x_N$ $y_N$

Output

Print the sum of all the scores modulo $998244353$.

4
0 0
0 1
1 0
1 1

5

We have five possible sets as $S$, four sets that form triangles and one set that forms a square. Each of them has a score of $2^0=1$, so the answer is $5$.

5
0 0
0 1
0 2
0 3
1 1

11

We have three "triangles" with a score of $1$ each, two "triangles" with a score of $2$ each, and one "triangle" with a score of $4$. Thus, the answer is $11$.

1
3141 2718

0

There are no possible set as $S$, so the answer is $0$.