Score : $900$ points

Problem Statement

Mole decided to live in an abandoned mine. The structure of the mine is represented by a simple connected undirected graph which consists of $N$ vertices numbered $1$ through $N$ and $M$ edges. The $i$-th edge connects Vertices $a_i$ and $b_i$, and it costs $c_i$ yen (the currency of Japan) to remove it.

Mole would like to remove some of the edges so that there is exactly one path from Vertex $1$ to Vertex $N$ that does not visit the same vertex more than once. Find the minimum budget needed to achieve this.

Constraints

• $2 \leq N \leq 15$
• $N-1 \leq M \leq N(N-1)/2$
• $1 \leq a_i, b_i \leq N$
• $1 \leq c_i \leq 10^{6}$
• There are neither multiple edges nor self-loops in the given graph.
• The given graph is connected.

Input

Input is given from Standard Input in the following format:

$N$ $M$

$a_1$ $b_1$ $c_1$

$:$

$a_M$ $b_M$ $c_M$

Output

Print the answer.

4 6
1 2 100
3 1 100
2 4 100
4 3 100
1 4 100
3 2 100

200

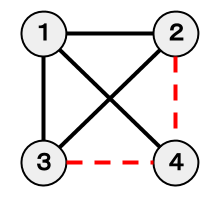
By removing the two edges represented by the red dotted lines in the figure below, the objective can be achieved for a cost of $200$ yen.

2 1
1 2 1

0

It is possible that there is already only one path from Vertex $1$ to Vertex $N$ in the beginning.

15 22
8 13 33418
14 15 55849
7 10 15207
4 6 64328
6 9 86902
15 7 46978
8 14 53526
1 2 8720
14 12 37748
8 3 61543
6 5 32425
4 11 20932
3 12 55123
8 2 45333
9 12 77796
3 9 71922
12 15 70793
2 4 25485
11 6 1436
2 7 81563
7 11 97843
3 1 40491

133677