atcoder#ARC062C. [ARC062E] AtCoDeerくんと立方体づくり
[ARC062E] AtCoDeerくんと立方体づくり
Score : points
Problem Statement
AtCoDeer the deer has square tiles. The tiles are numbered through , and the number given to each tile is written on one side of the tile. Also, each corner of each tile is painted in one of the colors, which are represented by the integers between . The top-left, top-right, bottom-right and bottom-left corner of the tile with the number are painted in color and , respectively, when seen in the direction of the number written on the tile (See Figure ).
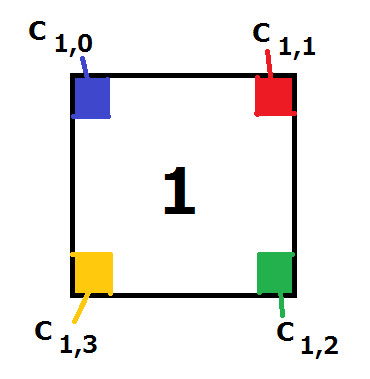
Figure : The correspondence between the colors of a tile and the input
AtCoDeer is constructing a cube using six of these tiles, under the following conditions:
- For each tile, the side with the number must face outward.
- For each vertex of the cube, the three corners of the tiles that forms it must all be painted in the same color.
Help him by finding the number of the different cubes that can be constructed under the conditions. Since each tile has a number written on it, two cubes are considered different if the set of the used tiles are different, or the tiles are used in different directions, even if the formation of the colors are the same. (Each tile can be used in one of the four directions, obtained by rotations.) Two cubes are considered the same only if rotating one in the three dimensional space can obtain an exact copy of the other, including the directions of the tiles.
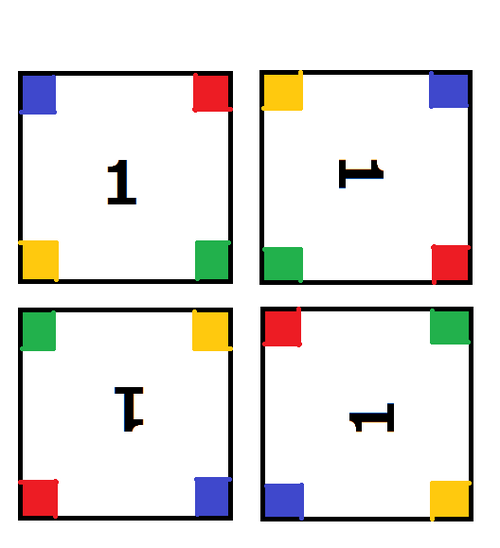
Figure : The four directions of a tile
Constraints
- $0 \leq C_{i,j} \leq 999 (1 \leq i \leq N , 0 \leq j \leq 3)$
Input
The input is given from Standard Input in the following format:
Output
Print the number of the different cubes that can be constructed under the conditions.
6
0 1 2 3
0 4 6 1
1 6 7 2
2 7 5 3
6 4 5 7
4 0 3 5
1
The cube below can be constructed.
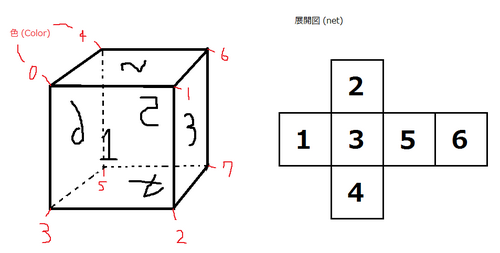
8
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 1
144
6
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
122880
