atcoder#ARC059C. [ARC059E] キャンディーとN人の子供
[ARC059E] キャンディーとN人の子供
Score : points
Problem Statement
12:17 (UTC): The sample input 1 and 2 were swapped. The error is now fixed. We are very sorry for your inconvenience.
There are children in AtCoder Kindergarten, conveniently numbered through . Mr. Evi will distribute indistinguishable candies to the children.
If child is given candies, the child's happiness will become , where is the child's excitement level. The activity level of the kindergarten is the product of the happiness of all the children.
For each possible way to distribute candies to the children by giving zero or more candies to each child, calculate the activity level of the kindergarten. Then, calculate the sum over all possible way to distribute candies. This sum can be seen as a function of the children's excitement levels , thus we call it .
You are given integers . Find 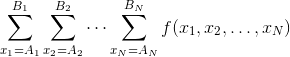
modulo .
Constraints
Partial Score
- points will be awarded for passing the test set satisfying .
Input
The input is given from Standard Input in the following format:
...
...
Output
Print the value of 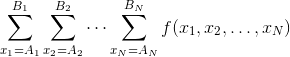
modulo .
2 3
1 1
1 1
4
This case is included in the test set for the partial score, since . We only have to consider the sum of the activity level of the kindergarten where the excitement level of both child and child are ().
- If child is given candy, and child is given candies, the activity level of the kindergarten is .
- If child is given candy, and child is given candies, the activity level of the kindergarten is .
- If child is given candies, and child is given candy, the activity level of the kindergarten is .
- If child is given candies, and child is given candy, the activity level of the kindergarten is .
Thus, , and the sum over all is also .
1 2
1
3
14
Since there is only one child, child 's happiness itself will be the activity level of the kindergarten. Since the only possible way to distribute candies is to give both candies to child , the activity level in this case will become the value of .
- When the excitement level of child is , .
- When the excitement level of child is , .
- When the excitement level of child is , .
Thus, the answer is .
2 3
1 1
2 2
66
Since it can be seen that , the answer is .
4 8
3 1 4 1
3 1 4 1
421749
This case is included in the test set for the partial score.
3 100
7 6 5
9 9 9
139123417
