atcoder#AGC016C. [AGC016C] +/- Rectangle
[AGC016C] +/- Rectangle
Score : points
Problem Statement
You are given four integers: , , and (, ). Determine whether there exists a matrix such that all of the following conditions are held, and construct one such matrix if the answer is positive:
- The matrix has rows and columns.
- Each element of the matrix is an integer between and (inclusive).
- The sum of all the elements of the matrix is positive.
- The sum of all the elements within every subrectangle with rows and columns in the matrix is negative.
Constraints
Input
Input is given from Standard Input in the following format:
Output
If there does not exist a matrix that satisfies all of the conditions, print No.
Otherwise, print Yes in the first line, and print a matrix in the subsequent lines in the following format:
Here, represents the element of the matrix.
3 3 2 2
Yes
1 1 1
1 -4 1
1 1 1
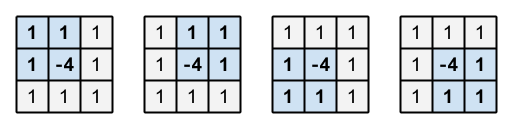
The sum of all the elements of this matrix is , which is positive. Also, in this matrix, there are four subrectangles with rows and columns as shown below. For each of them, the sum of all the elements inside is , which is negative.
2 4 1 2
No
3 4 2 3
Yes
2 -5 8 7
3 -5 -4 -5
2 1 -1 7
