atcoder#AGC006B. [AGC006B] Median Pyramid Easy
[AGC006B] Median Pyramid Easy
Score : points
Problem Statement
We have a pyramid with steps, built with blocks. The steps are numbered through from top to bottom. For each , step consists of blocks aligned horizontally. The pyramid is built so that the blocks at the centers of the steps are aligned vertically.
A pyramid with steps
Snuke wrote a permutation of (, , , ) into the blocks of step . Then, he wrote integers into all remaining blocks, under the following rule:
- The integer written into a block must be equal to the median of the three integers written into the three blocks directly under , or to the lower left or lower right of .
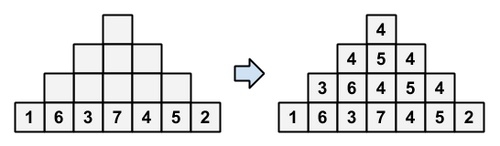
Writing integers into the blocks
Afterwards, he erased all integers written into the blocks. Now, he only remembers that the integer written into the block of step was .
Construct a permutation of (, , , ) that could have been written into the blocks of step , or declare that Snuke's memory is incorrect and such a permutation does not exist.
Constraints
Input
The input is given from Standard Input in the following format:
Output
If no permutation of (, , , ) could have been written into the blocks of step , print No.
Otherwise, print Yes in the first line, then print lines in addition.
The -th of these lines should contain the -th element of a possible permutation.
4 4
Yes
1
6
3
7
4
5
2
This case corresponds to the figure in the problem statement.
2 1
No
No matter what permutation was written into the blocks of step , the integer written into the block of step would be .
