配点 : $200$ 点

問題文

$xy$ 平面上に、左下の座標が $(0, 0)$、右上の座標が $(W, H)$ で、各辺が $x$ 軸か $y$ 軸に平行な長方形があります。最初、長方形の内部は白く塗られています。

すぬけ君はこの長方形の中に $N$ 個の点を打ちました。$i$ 個目 ($1 \leq i \leq N$) 点の座標は $(x_i, y_i)$ でした。

また、すぬけ君は長さ $N$ の数列 $a$ を決めて、各 $1 \leq i \leq N$ に対し、

• $a_i = 1$ のときは長方形の $x < x_i$ をみたす領域
• $a_i = 2$ のときは長方形の $x > x_i$ をみたす領域
• $a_i = 3$ のときは長方形の $y < y_i$ をみたす領域
• $a_i = 4$ のときは長方形の $y > y_i$ をみたす領域

を黒く塗りました。

塗りつぶしが終わったあとの長方形内での白い部分の面積を求めてください。

制約

• $1 \leq W, H \leq 100$
• $1 \leq N \leq 100$
• $0 \leq x_i \leq W$ ($1 \leq i \leq N$)
• $0 \leq y_i \leq H$ ($1 \leq i \leq N$)
• $W$, $H$ (21:32 追記), $x_i$, $y_i$ は整数である
• $a_i$ ($1 \leq i \leq N$) は $1, 2, 3, 4$ のいずれかである

入力

入力は以下の形式で標準入力から与えられる。

$W$ $H$ $N$

$x_1$ $y_1$ $a_1$

$x_2$ $y_2$ $a_2$

$:$

$x_N$ $y_N$ $a_N$

出力

塗りつぶしが終わったあとの長方形内での白い部分の面積を出力せよ。

5 4 2
2 1 1
3 3 4

9

すぬけ君が塗りつぶしを始める前の長方形は以下の図のようになっています。

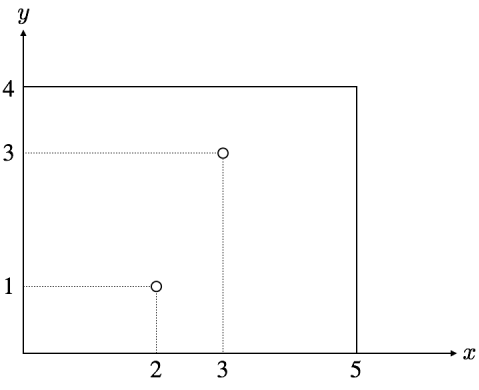
$(x_1, y_1) = (2, 1)$、$a_1 = 1$ なので、まずすぬけ君は $x$ 座標が $2$ より小さい領域を塗りつぶし、長方形は以下のようになります。

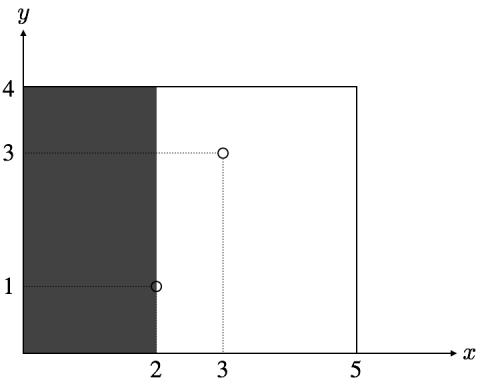
$(x_2, y_2) = (3, 3)$、$a_2 = 4$ なので、次にすぬけ君は $y$ 座標が $3$ より大きい領域を塗りつぶし、長方形は最終的に以下のようになります。

この最終的な状態における白い部分の面積は $9$ なので、出力は $9$ となります。

5 4 3
2 1 1
3 3 4
1 4 2

0

塗りつぶした結果、白い部分が残らないこともありえます。

10 10 5
1 6 1
4 1 3
6 9 4
9 4 2
3 1 3

64