[NOIP 2002 普及组] 过河卒

0
快乐baylor LV 3 @ 2025-4-20 18:27:54
一道比较入门的 dp 题

这道题初始位置是从 0 开始的，这样不是很利于我们解题，所以不如暂且把这题里涉及的坐标统统 +1，那么初始位置就从 $(0,0)$ 变成了 $(1,1)$ 。

先考虑如果没有任何马的限制，卒子可以随便向右向下走，那么可以想到，一个卒子只能从当前格子的左侧格子和当前格子的上方格子上走到当前格子。那么假设从 $(1,1)$ 走到当前格子的左侧格子的路径条数是 $x$ ，从 $(1,1)$ 走到当前格子的上方格子的路径条数是 $y$ ，那么从 $(1,1)$ 走到当前格子的路径条数就应该是 $x+y$ 。

其实我们已经得到了一个动态规划的转移方程，设 $f(i,j)$ 表示从 $(1,1)$ 格子走到当前格子的路径条数，那么根据上一段得到的结论，可以得到：
$f(i,j) = f(i-1,j) + f(i,j-1)$
$(i,j)$ 是当前格子，那么 $(i-1,j)$ 就是当前格子的上方格子， $(i,j-1)$ 就是当前格子的左侧格子。我们只需要从小到大依次枚举 $i$ 和 $j$ 就能获得所有点的答案，可以想到，在这道题里我们要求的答案就是 $f(n,m)$ （因为 B 点的坐标是 $(n,m)$ ）。

当然如果只是按照这个公式推肯定不行，因为 $f$ 的初始数值都是 0，再怎么推也都是 0，我们要让 $f(1,1)$ 能根据上面得到的式子推出答案是 1，这样才能有有意义的结果。根据 $f(1,1)=f(0,1)+f(1,0)$ ，我们只需要让 $f(1,0)=1$ 或者 $f(0,1)=1$ 即可。

接下来考虑一下加入了马这道题该怎么做，假设 $(x,y)$ 这个点被马拦住了，其实就是说这个点不能被卒子走到，那当我们枚举到这个点的时候，发现他被马拦住了，那就直接跳过这个点，让 $f(x,y)=0$ 就行了。

具体写代码的时候我们注意到在判断一个点有没有被马拦住时，会用到 $(i-2,j-1)$ 和 $(i-1,j-2)$ 这两个位置，那如果不把所有的点的坐标都加上 2 （前面分析的时候只把所有的坐标加上 1），就会因为数组越界而 WA 掉一个点。

答案可能很大，所以记得开 long long。
```
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;

const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
//马可以走到的位置

int bx, by, mx, my;
ll f[40][40];
bool s[40][40]; //判断这个点有没有马拦住
int main(){
    scanf("%d%d%d%d", &bx, &by, &mx, &my);
    bx += 2; by += 2; mx += 2; my += 2;
    //坐标+2以防越界
    f[2][1] = 1;//初始化
    s[mx][my] = 1;//标记马的位置
    for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;
    for(int i = 2; i <= bx; i++){
        for(int j = 2; j <= by; j++){
            if(s[i][j]) continue; // 如果被马拦住就直接跳过
            f[i][j] = f[i - 1][j] + f[i][j - 1];
            //状态转移方程
        }
    }
    printf("%lld\n", f[bx][by]);
    return 0;
} 
```
考虑滚动数组优化。

观察转移方程 :
$f(i,j) = f(i-1,j) + f(i,j-1)$
每一次转移只需要提供 $f(i-1,j)$ 和 $f(i,j-1)$ 。

即当前位置上方格子的答案与当前位置左边的答案，也就是说，对于一次转移，我们只需要用到横坐标是 $i$ 和横坐标是 $i-1$ 这两行的答案，其他位置的答案已经是没有用处的了，我们可以直接丢掉不管他们。

怎么只保留第 $i$ 行和第 $i-1$ 行的答案呢？答案是取模（C++ 中的运算符 %）。

$i\ \%\ 2\ne (i-1)\ \%\ 2$ ，所以我们把第一维的坐标 $i$ 都取模 2 变成 $i\ \%\ 2$ ，并且不断覆盖原来数组里存的答案，就成功做到只保留第 $i$ 行和第 $i-1$ 行的答案了。

众所周知， $x\ \%\ 2$ 可以在代码中写成更快的运算方式 $i\ \&\ 1$ 。

如果 $x$ 是偶数，那么 $x\ \&\ 1=0$ ，如果 $x$ 是奇数，那么 $x\ \&\ 1=1$ 。

那么新的转移方程就可以变成：
$f(0,1)=1$ $f(i\ \&\ 1,j)=f((i-1)\ \&\ 1,j)+f(i\ \&\ 1,j-1)$
$f((i-1)\ \&\ 1,j)$ 就是当前位置上边格子的答案。

$f(i\ \&\ 1,j-1)$ 就是当前位置左边的答案。

这样 , 数组第一维是不是就可以压成 2 了呢？

另外 , 因为是滚动数组 , 所以如果当前位置被马拦住了一定要记住清零。

代码 :
```
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#define ll long long
using namespace std;

const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};
int bx, by, mx, my;
ll f[2][40];    //第一维大小为 2 就好
bool s[40][40];

int main(){
    scanf("%d%d%d%d", &bx, &by, &mx, &my);
    bx += 2; by += 2; mx += 2; my += 2;
    f[1][2] = 1; //初始化
    s[mx][my] = 1;
    for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;
    for(int i = 2; i <= bx; i++){
        for(int j = 2; j <= by; j++){
            if(s[i][j]){
                f[i & 1][j] = 0; //被马拦住了记住清零
                continue;
            }
            f[i & 1][j] = f[(i - 1) & 1][j] + f[i & 1][j - 1]; 
            //新的状态转移方程
        }
    }
    printf("%lld\n", f[bx & 1][by]);
    //输出的时候第一维也要按位与一下
    return 0;
} 
```
好的那继续来看看能不能再优化。

唯一再有点优化空间的地方就是那个大小为 2 的第一维了，那么为什么我们去不掉这个 2 呢？

因为状态转移的时候需要一个 $f(i-1,j)$ ，所以必须要多开一维。

那么我们如果优化掉了这里，当然就不再需要二维数组了。

观察我们能发现 , 这个 $f(i-1,j)$ 与当前位置的 $f(i,j)$ 的第二维一样 , 都是 j , 而第一维只是差了 1。

我们考虑直接去掉第一维，来看这个状态转移方程 :
$f(j) = f(j) + f(j-1)$
是不是就把数组变成一维了呢？但是如何解释这个方程？

$f(j)+f(j-1)$ 里面， $f(j-1)$ 就是前面方程里的 $f(i,j-1)$ 。

至于 $f(j)$ , 因为还没有被更新过 , 所以答案仍然保存的是上次求出的答案 , 即 $f(i-1,j)$ 。

这样 , 就把二维数组成功变成了一维数组。

代码 :
```
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;

// 快速读入
template <class I>
inline void read(I &num){
    num = 0; char c = getchar(), up = c;
    while(!isdigit(c)) up = c, c = getchar();
    while(isdigit(c)) num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();
    up == '-' ? num = -num : 0; return;
}
template <class I>
inline void read(I &a, I &b) {read(a); read(b);}
template <class I>
inline void read(I &a, I &b, I &c) {read(a); read(b); read(c);}

const int fx[] = {0, -2, -1, 1, 2, 2, 1, -1, -2};
const int fy[] = {0, 1, 2, 2, 1, -1, -2, -2, -1};

int bx, by, mx, my;
ll f[40];   //这次只需要一维数组啦
bool s[40][40];

int main(){
    read(bx, by); read(mx, my);
    bx += 2; by += 2; mx += 2; my += 2;
    f[2] = 1;   //初始化
    s[mx][my] = 1;
    for(int i = 1; i <= 8; i++) s[mx + fx[i]][my + fy[i]] = 1;
    for(int i = 2; i <= bx; i++){
        for(int j = 2; j <= by; j++){
            if(s[i][j]){
                f[j] = 0; // 还是别忘了清零
                continue;
            }
            f[j] += f[j - 1];
            //全新的 简洁的状态转移方程
        }
    }
    printf("%lld\n", f[by]);
    return 0;
} 
```
这时可能就有同学说了，f 数组是变成一维了，但是你的 s 数组还是二维的啊你个骗子！

至于去掉 s 数组的方法，其实还是很多的。

首先有比较暴力的方法，我们直接去掉 s 数组，然后对于当前位置 $(x,y)$ ，我们枚举被马拦住的那 8 个点，如果其中有一个点的位置和他的位置是一样的，那么这个位置就是不合法的了。这个方法可行，但是我们把本来是 $O(n^2)$ 小常数的做法加了一个 8 倍常数。如果把范围开大到 $n\leq 2\times 10^4$ ，那么这个做法可能会被卡。

有没有别的方法呢？下面可能会用到这个知识点：切比雪夫距离。

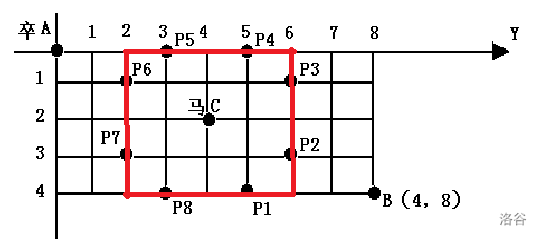
我们注意到，被马拦住的位置到马的切比雪夫距离一定是2，也就是说，他们都分布于下图这个正方形上，那我们就成功缩小了枚举范围：只有当当前这个点 $(x,y)$ 到马的切比雪夫距离是 2 时，才进行 8 个点的枚举，那么复杂度大概就是 $O(n^2+16\times 8)$ （原谅我用这种不正确的方法书写复杂度），常数很小。

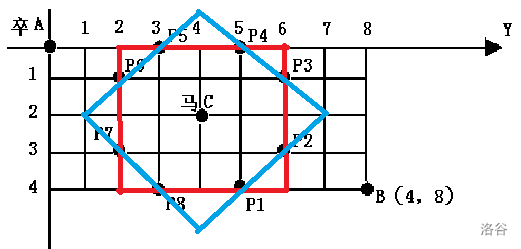
但是还能有更好的方法，那就是加上曼哈顿距离：我们可以发现，这些被马拦住的位置同时到马的曼哈顿距离也一定为 3。

蓝色是曼哈顿距离为 3 的位置，红色是切比雪夫距离为 2 的位置，交点是被马拦住的位置，且被马拦住的位置一定是交点，也就是说，这是个充要条件。

所以对于每个点我们只需要算一下他到马的切比雪夫距离和曼哈顿距离即可，这个计算都是 $O(1)$ 的，且常数很小。
```
#include <cmath>
#include <cctype>
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ll long long

inline int read(){
    int num = 0; char c = getchar();
    while(!isdigit(c)) c = getchar();
    while(isdigit(c)) num = (num << 1) + (num << 3) + (c ^ '0'), c = getchar();
    return num;
}

int bx, by, mx, my;
ll f[30];

inline bool check(int x, int y) {
    if(x == mx && y == my) return 1;
    return (std::abs(mx - x) + std::abs(my - y) == 3) && (std::max ((std::abs(mx - x)), std::abs(my - y)) == 2);
}

int main(){
    bx = read() + 2, by = read() + 2, mx = read() + 2, my = read() + 2;
    f[2] = 1;
    for(int i = 2; i <= bx; i++){
        for(int j = 2; j <= by; j++){
            if(check(i, j)){
                f[j] = 0;
                continue;
            }
            f[j] += f[j - 1];
        }
    }
    printf("%lld\n", f[by]);
    return 0;
} 
```
至此，我们成功将一个时间复杂度和空间复杂度为 $O(n^2)$ 的算法，优化到了时间复杂度 $O(n^2)$ ，空间复杂度 $O(n)$ ，虽然对于这道题而言没有任何的意义，但是或许能在做其他难题的时候启发我们一点思路，总归是没有坏处的。