该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

究竟谁获胜？

时间限制：1s

空间限制：256 MB

题目描述

有一个由 $n\times n$ 个边长为 $1$ 的小正方形组成的网格，zms 和 jrm 在此基础上进行比赛，比赛的规则如下：

• zms 和 jrm 轮流进行操作，zms 先手。
• 当 zms 操作时，选择一条尚未被染色的正方形边框并将其染成 红色。操作结束时，如果这条边框是一个（或两个）正方形最后一条被染色的边框，则自动将该正方形也同样染成 红色。
• 当 jrm 操作时，选择一条尚未被染色的正方形边框并将其染成 蓝色。操作结束时，如果这条边框是一个（或两个）正方形最后一条被染色的边框，则自动将该正方形也同样染成 蓝色。
• 当所有的边框都被染色后，游戏结束。此时染成自己所属颜色的正方形数量更多的获胜；或者当数量相等时，达成平局。

例如，在 $2\times 2$ 的网格图中，一种可能的游戏过程如下：

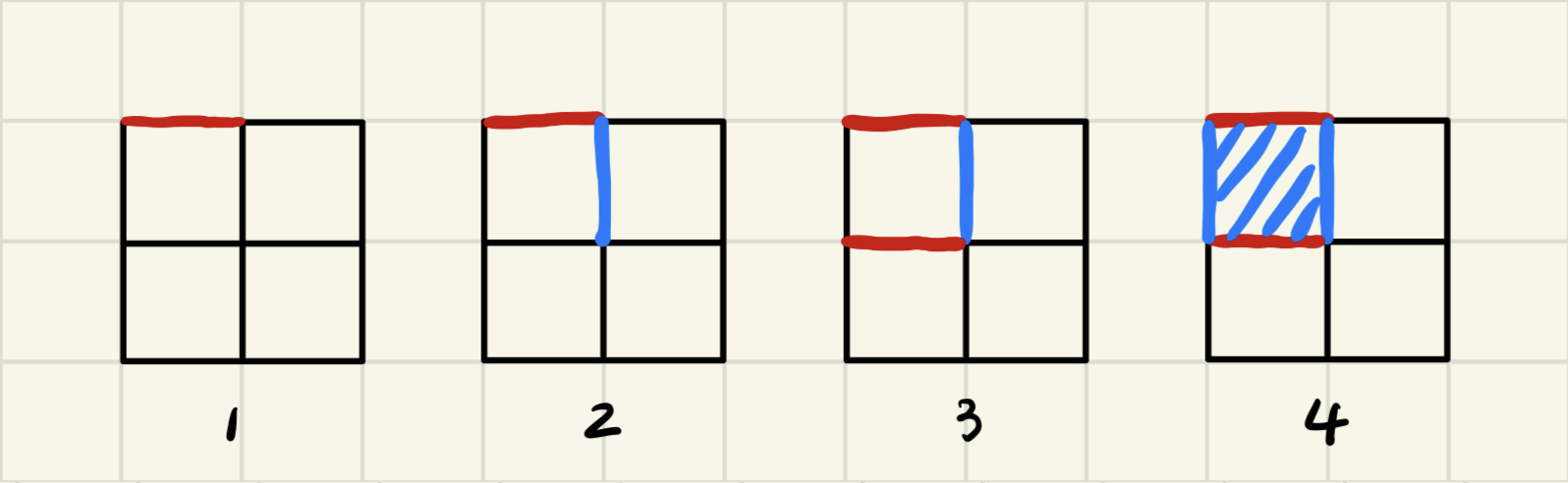
已知网格图的边长 $n$，如果两人都按照最优策略进行比赛（尽可能地让自己获胜，或者在自己无法获胜的前提下尽可能地达成平局），请你推断哪一方会获胜或达成平局。

输入格式

一行包含一个整数 $n\ (1\le n\le 10^9$)，表示网格图的边长。

输出格式

如果 zms 获胜，输出 'zms'（不带引号，下同）；否则如果 jrm 获胜，输出 'jrm'；否则平局输出 'tie'。

样例输入

2

样例输出

jrm

数据范围与约定

$1\le n\le 10^9$ 。