该比赛已结束，您无法在比赛模式下递交该题目。您可以点击“在题库中打开”以普通模式查看和递交本题。

康托三分集

时间限制：1s​

空间限制：256MB​

题目背景

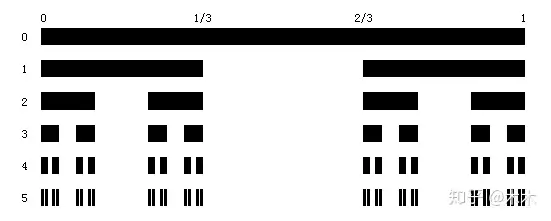
康托$(G.Cantor)$在$1883$年构造了如下的一类集合。选取一个欧氏长度为$1$的直线段，将该线段三等分，去掉中间一段，剩下两段。将剩下的两段分别在三等分，各去掉中间一段。剩下四段。将这样的操作继续下去，直至无穷，则可得到一个离散的点集，点数趋于无穷多，而欧氏长度趋于零。经无数次操作，达到极限时所得到的离散点集称之为康托三分集（如图所示）。

题目描述

可莉在不久前在嘟嘟可上刷到了康托三分集相关的内容，并对此十分好奇，想要知道一个小数$F$会在第几层消失。

在第$k$层消失指的是，$F$在前$k-1$操作中都没有被去掉，并且在第$k$次操作中被去掉了。

如果这个数在充分多次操作后仍然没有被去掉，请你回答"$\text-1$".

输入格式

第一行，一个正整数$T$，表示测试用例的个数。$T \le 10^5$.

每个测试用例一行，两个整数$p,q$表示小数$\frac{p}{q}$，数据保证$1 \le p,q \le 10^9$.

输出格式

输出$k$，表示小数$\frac{p}{q}$在第$k$行消失.如果$k\rightarrow +\infty$，输出$-1$.

样例输入

5
133153156 3486784401
1 2
4 9
1 3
16 27

样例输出

3
1
1
-1
1

数据范围与约定

对于所有数据，$1 \le T \le 10^5,1 \le p,q \le 10^9$.

对于$25\%$的数据，$p=1$.

对于$25\%$的数据，$q = 3^k,k\in N$.

对于$50\%$的数据，没有限制。

上述三部分独立，总计$100\%$.