uoj#P604. 【UER #9】赶路
【UER #9】赶路
作为文化课大师,skip 蚤每天早上要从家里去学校。
然而,在去学校的路途中,它还要去 早饭店、女朋友家、公交车站、小卖部 等地方,它做了一定的统计,列出了一张单子,这张单子包含了 $n$ 个二维平面上的点,其中 $1$ 号地点是家,$n$ 号地点是学校。skip 蚤需要找到一个排列 $p$ 来描述它每天上学走的路线,其中 $p_i$ 表示它经过的第 $i$ 个地点,其中 $p_1 = 1, p_n = n$。
对于一个排列 $p$,skip 蚤会从笔直的从点 $p_i$ 走到 $p_{i+1}$。skip 蚤非常讨厌重复经过一个地方,所以它不能重复经过这个二维平面上的同一个点,即它的上学路线不能自交。
由于某些神秘的原因,不存在两个地点坐标相同,不存在三个地点都在某一条直线上。
输入格式
本题有多组测试数据,输入文件的第一行包含一个正整数 $T$,表示测试数据的组数。接下来包含恰好 $T$ 组测试数据,每组测试数据具有以下的格式:
第一行一个正整数 $n$ 表示地点数。
下面 $n$ 行,每行两个整数 $x_i, y_i$,表示地点 $i$ 在二维平面的坐标是 $(x_i, y_i)$。
输出格式
输出包含 $T$ 行,分别表示 $T$ 组测试数据的答案。
对于每组数据,如果不存在合法路径,在该行输出 -1。否则,输出一行 $n$ 个正整数,表示一个排列 $p$,其中 $p_i$ 是 skip 蚤第 $i$ 个到达的地点的编号,如果有多种方案,请任意输出一种。
1
4
3 3
4 3
4 4
3 2
1 3 2 4
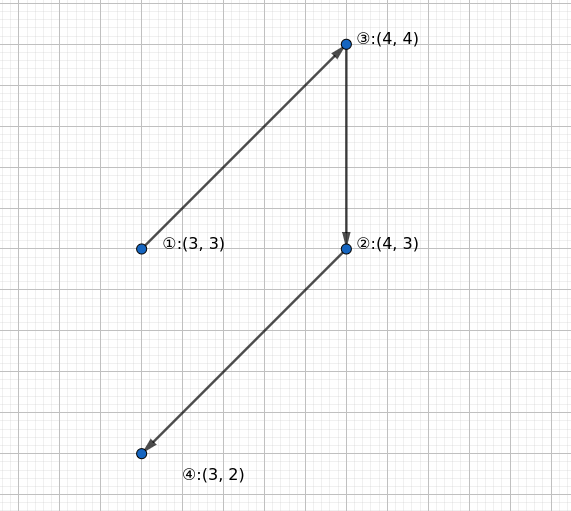
如图所示,容易发现这是一组合法的方案。
样例二
见附加文件中 ex_easy2.in,输出不下发但依然可以提交测试该样例。
样例三
见附加文件中 ex_easy3.in,输出不下发但依然可以提交测试该样例。
限制与约定
对于所有数据,保证 $2 \leq n \leq 500, -10^8 \leq x_i, y_i \leq 10^8, 1 \leq T \leq 30$。
| 测试点编号 | $n\leq$ | 特殊性质 |
|---|---|---|
| $1$ | $10$ | 无 |
| $2$ | ||
| $3$ | $15$ | |
| $4$ | ||
| $5$ | $500$ | $x_1 = y_1 = 0$ 且四个象限均存在点 |
| $6$ | $x_1 \leq x_i \leq x_n$ | |
| $7$ | ||
| $8$ | 无 | |
| $9$ | ||
| $10$ |
时间限制:$1\texttt{s}$
空间限制:$512\texttt{MB}$
