uoj#P482. 【NOI2019】斗主地
【NOI2019】斗主地
小 S 在和小 F 玩一个叫「斗地主」的游戏。
可怜的小 S 发现自己打牌并打不过小 F,所以他想要在洗牌环节动动手脚。
一副牌一共有 $n$ 张牌,从上到下依次标号为 $1 \sim n$。标号为 $i$ 的牌分数是 $f (i)$。在本题,$f (i)$ 有且仅有两种可能:$f (i) = i$ 或 $f (i) = i^2$。
洗牌的方式和我们日常生活中的比较类似,以下我们用形式化的语言来定义:
洗牌环节一共分 $m$ 轮,这 $m$ 轮洗牌依次进行。第 $i$ 轮洗牌时: 1. 小 S 会拿出从最上面往下数的前 $A_i$ 张牌。这样这副牌就被分成了两堆:第一堆是最上面的 $A_i$ 张牌,第二堆是剩下的 $n − A_i$ 张牌,且这两堆牌内相对顺序不变。特别地,当 $A_i = n$ 或 $A_i = 0$ 时,有一堆牌是空的。 2. 接下来对两堆牌进行合并,从而产生新的第三堆牌。当第一堆牌还剩下 $X$ 张,第二堆牌还剩下 $Y$ 张的时候,以 $\frac{X}{X+Y}$ 的概率取出第一堆牌的最下面的牌,并将它放入新的第三堆牌的最上面,$\frac{Y}{X+Y}$ 的概率取出第二堆牌的最下面的牌,并将它放入新的第三堆牌的最上面。 3. 重复操作 2,一直取到两堆牌都为空为止。这样我们就完成了一轮洗牌。
因为洗牌过程是随机的,所以小 S 发现自己没法知道某个位置上具体是哪张牌。但小 S 想问你在经历了这 $m$ 轮洗牌后,某个位置上的牌的期望分数是多少。小 S 一共会问你 $Q$ 个这样的问题。
输入格式
从标准输入读入数据。
输入的第一行包含三个正整数 $n, m, \text{type}$,分别表示牌的数量,洗牌的轮数与 $f (i)$ 的类型。当 $\text{type} = 1$ 时,$f (i) = i$。当 $\text{type} = 2$ 时,$f (i) = i^2$。
接下来一行,一共 $m$ 个整数,表示 $A_1 \sim A_m$。
接下来一行一个正整数 $Q$,表示小 S 的询问个数。
接下来 $Q$ 行,每行一个正整数 $c_i$,表示小 S 想要知道从上往下第 $c_i$ 个位置上的牌的期望分数。保证 $1 \le c_i \le n$。
输出格式
输出到标准输出中。
输出一共 $Q$ 行,每行一个整数,表示答案在模 $998244353$ 意义下的取值。
即设答案化为最简分式后的形式为 $\frac{a}{b}$,其中 $a$ 和 $b$ 互质。输出整数 $x$ 使得 $bx \equiv a\ (\text{mod}\ 998244353)$ 且 $0 \le x < 998244353$。可以证明这样的整数 $x$ 是唯一的。
4 1 1
3
1
1
249561090
两棵树相同,所以任意两个点都必须被给予相同的数,方案数为 $2$。
有 $\frac 1 4$ 的概率从上到下的最终结果是 $\{1, 2, 3, 4\}$。
有 $\frac{1}{4}$ 的概率从上到下的最终结果是 $\{1, 2, 4, 3\}$。
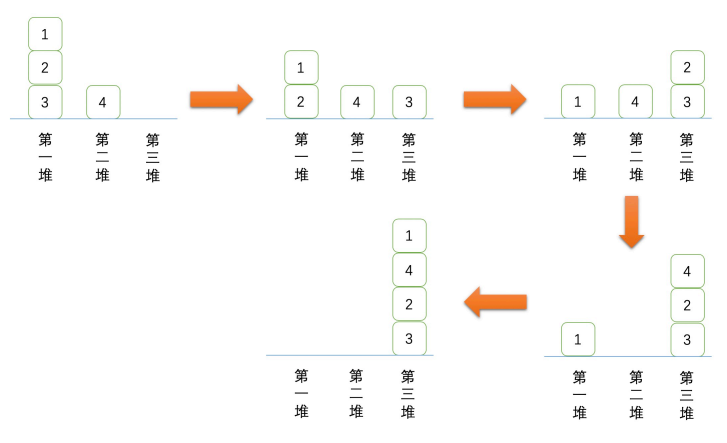
有 $\frac{1}{4}$ 的概率从上到下的最终结果是 $\{1, 4, 2, 3\}$。
有 $\frac{1}{4}$ 的概率从上到下的最终结果是 $\{4, 1, 2, 3\}$。
所以最终有 $\frac{1}{4}$ 的概率第一个位置是 $4$,有 $\frac{3}{4}$ 的概率第一个位置是 $1$,所以第一个位置的期望分数是 $\frac{7}{4}$。
为了帮助你们更直观地了解洗牌的过程,我们在下面画出了结果是 $\{1, 4, 2, 3\}$ 的过程:
样例二至样例三
见样例数据下载。
限制与约定
对于所有测试数据:$3 \le n \le 10^7 , 1 \le m, Q \le 5 \times 10^5 , 0 \le A_i \le n , \text{type} \in \{1, 2\}$。
| 测试点编号 | $n$ | $m$ | $\text{type}=$ | 其他性质 |
|---|---|---|---|---|
| $1$ | $\le 10$ | $\le 1$ | $1$ | 无 |
| $2$ | $\le 80$ | $\le 80$ | $1$ | 无 |
| $3$ | $\le 80$ | $\le 80$ | $2$ | 无 |
| $4$ | $\le 100$ | $5\times 10^5$ | $2$ | 所有$A_i$均相同 |
| $5$ | $10^7$ | $5\times 10^5$ | $1$ | 无 |
| $6$ | $10^7$ | $5\times 10^5$ | $1$ | 无 |
| $7$ | $10^7$ | $5\times 10^5$ | $1$ | 无 |
| $8$ | $10^7$ | $5\times 10^5$ | $2$ | 无 |
| $9$ | $10^7$ | $5\times 10^5$ | $2$ | 无 |
| $10$ | $10^7$ | $5\times 10^5$ | $2$ | 无 |
时间限制: 4s
空间限制: 512MB
