uoj#P114. 【UER #2】信息的交换
【UER #2】信息的交换
由于电信技术的发展,信息的交换变得十分方便。
现在有 $n$ 个人,依次编号为 $1, \dots, n$。初始时第 $i$ 个人手机里存储着编号为 $i$ 的气泡熊表情。由于对自己的表情并不十分满意,他们计划进行一次大交换。
这 $n$ 个人中有一些朋友关系,可以抽象为一个简单无向图 $G$。简单无向图即无重边无自环的无向图。
每个人有三种状态:不满,激动,满意。初始时均为不满。
有一个神秘人,操纵他们按如下方式行动:
function dfs(v):
v 变为激动状态
for u = 1, ..., n:
if v 和 u 是朋友 and u 处于不满状态:
交换 v 和 u 的手机中的气泡熊表情
dfs(u)
v 变为满意状态
for v = 1, ..., n:
if v 处于不满状态:
dfs(v)
一万万年后,一位考古学家调查了最终每个手机中存储的气泡熊表情的编号,想要复原出朋友关系图 $G$。然而这几乎是不可能的,所以他想知道有多少种可能的 $G$。
输入格式
第一行一个正整数 $n$。
第二行包含 $n$ 个整数 $a_1, \dots, a_n$,表示最终第 $i$ 个人的手机上存储的气泡熊表情编号。保证 $a_1, \dots, a_n$ 是一个 $1$ 到 $n$ 的排列。
输出格式
一行,一个整数表示 $G$ 的数量,你只用输出答案对 $998244353$($7 \times 17 \times 2^{23} + 1$,一个质数)取模后的结果。
3
2 3 1
2
共以下两种:
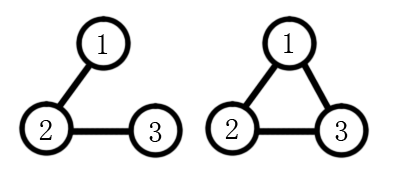
9
7 2 9 1 3 8 6 5 4
3528
样例三
见样例数据下载。
限制与约定
| 测试点编号 | $n$的规模 |
|---|---|
| 1 | $n \leq 6$ |
| 2 | $n \leq 9$ |
| 3 | |
| 4 | $n \leq 50$ |
| 5 | |
| 6 | |
| 7 | |
| 8 | $n \leq 500$ |
| 9 | |
| 10 |
时间限制:$1\texttt{s}$
空间限制:$256\texttt{MB}$
