题目背景

在 youyou 的班上，身高可能是一个敏感的话题。

题目描述

youyou 的班上一共有 $n$ 位同学，$m$ 对朋友，第 $i$ 对朋友关系对于身高有一个敏感值 $k_i$，敏感值可能会改变。

我们定义两位同学如果互为朋友，那么必然存在某对关系，将两位同学直接相连。

我们定义两位同学如果互为好友，那么必然存在直接或间接的关系，将两位同学相连。

例如存在关系 $(1,2)$ 和 $(2,3)$，那么，$1$ 与 $2$ 是朋友，但 $1$ 与 $3$ 就是好友。

现在，马上就要军训了，同学们要去领军训的服装，如果一位同学领到了尺码为 $p$ 的服装，所有同学会与朋友关系敏感值小于 $p$ 的朋友断交。即对于所有的朋友关系，若其敏感值小于 $p$，那么该朋友关系就会断开。不过在下一位同学领到服装时，所有之前的断开的朋友关系会恢复。

由于军训领服装是一个复杂的过程，而 youyou 对此十分感兴趣，所以给出 $q$ 次操作，且一共有三种操作:

• 操作 $1$，形如 1 x，表示有一位同学领到尺码为 $x$ 的服装。

• 操作 $2$，形如 2 x，表示询问第 $x$ 位同学还有多少位好友（包括自己）。

• 操作 $3$，形如 3 x y，表示第 $x$ 对朋友的敏感值变为 $y$，特别地，敏感值的相对大小不会变化$^*$（详情见下方），同时原来已经断开的关系不会恢复。

注意：好友跟朋友是两个概念，朋友一定是好友，但好友不一定是朋友。

$^*$：相对大小不会变化，指对于当前所有的敏感值而言，修改后的敏感值与原来的敏感值排名相同。

例如，若原来所有对朋友之间敏感值是 $\{1,2,3,5,6\}$，$3$ 的排名为 $3$，因此 $3$ 只能修改为 $3,4$ 中的一个，这样才能保证排名不变，即相对大小位置不会变换。

输入格式

第一行，输入三个正整数 $n,m,q$。

后面 $m$ 行，给定 $m$ 对朋友关系，对于第 $i$ 行给定三个正整数 $x_i,y_i,k_i$。

最后 $q$ 行，给定 $q$ 次操作。对于每次操作，给定一个正整数为 $op$，即操作类型。

当 $op=1$ 时，再给定一个正整数 $x$，表示有一位同学领到尺码为 $x$ 的服装；

当 $op=2$ 时，再给定一个正整数 $x$，表示一次询问；

当 $op=3$ 时，再给定两个正整数 $x,y$，表示一次修改。

输出格式

对于每次询问操作，输出一个 $x$ 表示询问的同学还有几位好友（包括自己）。保证对于每一个测试点，都会有一个询问操作。

4 3 3
1 2 156
1 4 42
2 3 0
1 26963
3 3 40
2 4

1

7 6 7
1 2 292
1 3 274
1 4 221
1 5 156
3 4 42
3 6 40
1 30
3 4 50
2 6
3 3 250
3 1 298
1 280
2 1

6
2

提示

样例解释 #1

如图所示，这是初始的关系图。

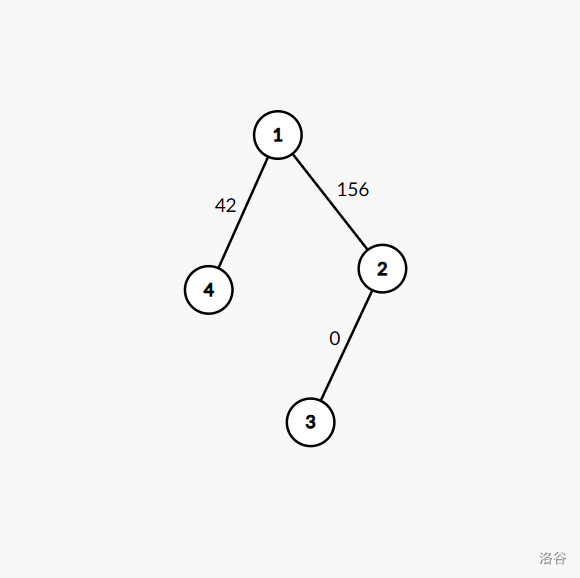
第一次操作为：有一位同学领到尺码为 $26963$ 的服装，这样，图中所有的边都会断开。

下一次操作：第三对朋友即边 $(2,3)$ 的权变为 $40$。

下一次操作：询问同学 $4$ 的好友数量，因为没有任何存在的边，因此答案为 $1$。

数据范围

测试点编号	$n$	$q$	特殊性质
$1,2$	$\le 10$	$\le 4 \times 10^5$	无
$3$	$\le 10^3$
$4$	$\le 10^5$	$\le 4 \times 10^5$	没有操作 $3$
$5,6$		$\le 10^3$	无
$7$		$\le 4 \times 10^5$	没有操作 $1$
$8,9,10$	$\le 4 \times 10^5$		无

用 $c_i$ 表示询问中同学领到服装尺码的大小，$e_i$ 表示修改后敏感值的大小。

对于 $100\%$ 的数据，$1 \le n,m,q,x_i,y_i \le 4 \times 10^5$，$1 \le k_i,c_i,e_i \le 1 \times 10^9$，$m\le \min\{\frac{n(n-1)}{2},4 \times 10^5\}$。

同时数据保证在任何时刻，所有对朋友关系之间的敏感值互不相同。

请注意常数因子对时间和空间产生的影响。