题目背景
那年你我仍是无瑕的少年
在夜晚安逸的后院无所顾忌地笑谈人生
——怀念这样毫无猜忌的时光
题目描述
悦,玲和荧三个人在湖底之城闲游。湖底之城的道路错综复杂,形成了一棵有 n 个节点的树。
她们三人的手上都有一个计数器,初始都为 0。她们每走到一个点的时候,悦和荧手上的计数器会自动加上刚刚经过的这条边的边权,同时玲的计数器会恰好增加 1。同时,她们整个过程中没有经过某个点超过一次。
由于她们的计数器不能存储很大的值,所以,当玲的计数器上的值是「湖之数」p 的倍数时,悦可以将她的计数器上的值减去荧的计数器上的值,接下来,玲和荧的计数器都会立刻归零。
玘现在不知道她们闲游的起点和终点,所以天生计算能力很好的玘对于每一对起点和终点,计算出了悦手上计数器在终点时可能出现的最小值。玘把这个值记作 f(u,v),意思是她们从点 u 走到了点 v。可是,玘认为,没有红色彼岸花的寒,一定是算不出来这些答案的。所以,他让寒做一道更简单的题。玘给寒一个长度为 m 的序列 s,让寒对于每一个点为 u 时计算 i=1minm{f(si,u)}。
形式化题面
给定一个 n 个点的树 (V,E) 和一个正整数 p,每一条边有一个整数边权 wi。
我们定义 f(s,v) 表示为对 u,a,b,c 进行若干次拓展后可以得到的当 u=v 时的 a 的最小值,其中最开始 u←s 同时 a,b,c←0。
拓展的定义为依次进行如下操作:
-
选择任意一条边 (u′,v,w)∈E 满足 u=u′,令 u←v,a←a+w,b←b+1,c←c+w;
-
如果 p∣b,你可以令 a←a−c,b←0,c←0。
特别地,对于每一次拓展,你不能取一个之前取过的点。
给定序列 {sm},对于每个点 u 求 i=1minm{f(si,u)}。
输入格式
第一行三个整数 n,m,p,表示树的节点数为 n,编号分别为 1∼n,「湖之数」为 p,序列 s 的长度为 m。
接下来 n−1 行每行三个整数 u,v,w 表示存在一条连接 u,v 两个点,边权为 w 的边。
接下来一行 m 个整数表示 s1∼m 即 m 个起点。
输出格式
设 ansu=i=1minm{f(si,u)},那么你需要输出 xori=1n∣ansi∣。其中 ∣a∣ 表示 a 的绝对值。
6 2 2
1 2 -2
1 3 1
1 4 2
2 5 -3
2 6 10
1 5
4
提示
样例解释
-
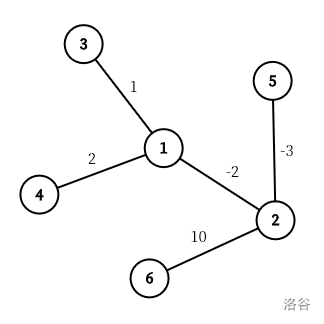
如果她们从 1 号点出发,首先有 f(1,1)=0。走到点 2,3,4 时悦的计数器上的值分别为 −2,1,2,所以 f(1,2)=−2,f(1,3)=1,f(1,4)=2。她们走到点 5,6 时,悦的计数器上的值分别为 −5,8。由于这时玲的计数器上的值等于 2,是 p 的倍数,所以悦可以选择让她手上的计数器的值减去荧的计数器的值,不难得出 f(1,5)=−5,f(1,6)=0。
-
如果她们从 5 号点出发,同理可得 $f(5,5)=0,f(5,2)=-3,f(5,6)=0,f(5,1)=-5,f(5,4)=-3,f(5,3)=-4$。
综上的 {ansn}={−5,−3,−4,−3,−5,0}。计算可得 xori=1n∣ansi∣=4。
数据范围
本题采用捆绑测试。
| 子任务编号 |
数据范围 |
特殊性质 |
分值 |
| Subtask1 |
m≤n≤100,p≤20 |
|
10 |
| Subtask2 |
m≤n≤103,p≤100 |
15 |
| Subtask3 |
n≤105,p≤100,m=1 |
10 |
| Subtask4 |
m≤n≤105,p=1 |
20 |
| Subtask5 |
m≤n≤105,p≤100 |
有 |
10 |
| Subtask6 |
|
35 |
特殊性质:保证树退化成一条链。
对于 100% 的数据 1≤m≤n≤105,1≤p≤100,−104≤w≤104,1≤u,v,si≤n。

