题目背景

ICPC2020 WF K

题目描述

Place-Y Technology Corp. plans to launch a new space station soon. The company CEO is known for being obsessed with perfection. For example, he insists that all the outer surfaces of the space station are regularly polished and cleaned of what he calls ``space debris,'' mainly for the station to appear good in photos. The engineering team tried but failed to convince the CEO that this was not needed. So instead they developed an innovative technology to maintain the surfaces while minimizing human operations outside the station. The maintenance is performed by several small robots moving over the space station surface, just like robotic vacuum cleaners. Before their first flight, Place-Y needs to assess the risks of collision during the operation of the robots. And this is exactly where you step in.

For the purposes of this problem, we model the space station as a collection of axis-aligned unit cubes (not necessarily connected). Each robot starts at time $t=0$ in the center of an exposed face of one of the station's unit cubes (that is, a face which is not shared by a second station cube). The robot is oriented in one of the four directions parallel to an edge of the cube face. Every time unit, the robot moves straight ahead to another cube face, possibly pivoting $90$ degrees across the space station edges so that it always maintains contact with the station. Note that if two cubes share an edge, the robot cannot slip between them (there is no gap).

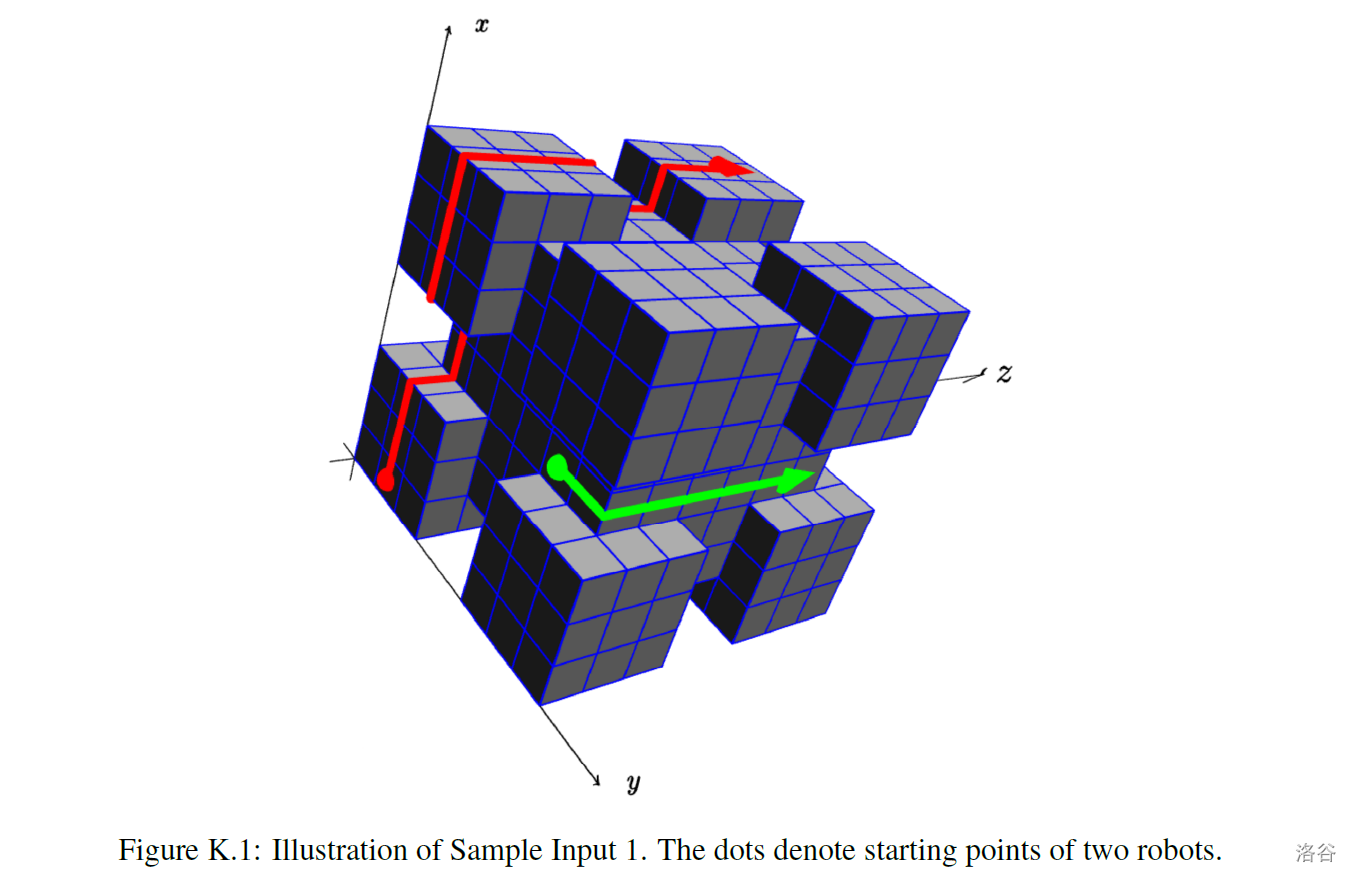
Given the layout of the station and starting positions of all the cleaning robots, determine the time of the earliest collision (if any). The time a collision occurs is either the time unit when two or more robots are on the interior of the same cube face or the time unit when two robots attempt to swap locations (see Sample Input 3 for the latter case).

输入格式

The first line of input contains two integers $n$ and $k$, where $n$ ($1 \le n \le 100$) is the number of regions describing the space station shape, and $k$ ($0 \le k \le 100$) is the number of robots on the surface.

Each of the following $n$ lines contains six integer coordinates $x_1$, $y_1$, $z_1$, $x_2$, $y_2$, and $z_2$ ($0 \le x_1 < x_2 \le 10^6$, $0 \le y_1 < y_2 \le 10^6$, $0 \le z_1 < z_2 \le 10^6$) describing one region and denoting that all the points $x,y,z$ satisfying $x_1 \le x \le x_2$, $y_1 \le y \le y_2$, $z_1 \le z \le z_2$ are part of the space station. Note that some unit cubes may be included in more than one region.

Then follow $k$ lines, each describing the starting position of one robot. Such a line contains three coordinates $x$, $y$, and $z$, and two directions $\vec{f}$ and $\vec{d}$. The coordinates specify that the robot starts at a face of the unit cube $(x,y,z) - (x+1,y+1,z+1)$. The particular face is determined by $\vec{f}$ and the initial direction of movement is determined by $\vec{d}$. Both $\vec{f}$ and $\vec{d}$ are specified by one of the six strings $\tt x+$, $\tt x-$, $\tt y+$, $\tt y-$, $\tt z+$, or $\tt z-$, where $\tt x+$ designates the positive direction of the x-axis $(1,0,0)$, and so on. The axis letter in $\vec{f}$ will be different from the axis letter in $\vec{d}$. It is guaranteed that the starting cube belongs to the space station and the given face is an exposed face.

输出格式

Output the time of the first collision. If there will never be a collision, output $\tt ok$.

题目大意

输入格式

每个机器人每次启动一开始t=0 每次机器人到另一个面，可能会旋转90°两个立方体共享一条边时，机器人无法在之间走动。

第一行输入n,k,n是空间站形状的区域数,k是机器人的数量。

接下来n行6个数据分别是：($0 \le x_1 < x_2 \le 10^6$, $0 \le y_1 < y_2 \le 10^6$, $0 \le z_1 < z_2 \le 10^6$)

是一个区域中的所有点。满足$x_1 \le x \le x_2$, $y_1 \le y \le y_2$, $z_1 \le z \le z_2$ 请注意，一些立方体可能包含在多个区域中。

接下来k行，每一行代表机器人的位置。有x,y,z以及两个方向f,d,指定面由f确定,初始移动方向由d确定.六种操作x+,x-,y+,y-,z+,z-. x+表示（1,0,0）的方向，依此类推。f不等于d.

保证起始立方体属于空间站，并且给定的初始面是外面。

输出格式

输出第一次碰撞的时间。如果永远不会发生冲突，则输出ok

9 2
1 1 1 7 7 7
0 0 0 3 3 3
5 0 0 8 3 3
0 5 0 3 8 3
0 0 5 3 3 8
5 5 0 8 8 3
5 0 5 8 3 8
0 5 5 3 8 8
5 5 5 8 8 8
0 1 0 z- x+
3 5 1 z- y+

44

1 3
0 0 0 1 1 1
0 0 0 x+ z+
0 0 0 y+ x+
0 0 0 z- y+

ok

1 2
0 0 0 2 1 1
0 0 0 y+ x+
1 0 0 y+ x-

0