题目描述
给定一个正整数 n 个一个满足 2i(i−1)<ai≤2i(i+1) 的正整数序列 a1,a2,⋯,an。
该序列是一棵包含 2(n+1)(n+2) 个节点的树参数化而来的,它包括 n+1 层,每层分别包括 1,2,⋯,n+1 个节点,如图所示:
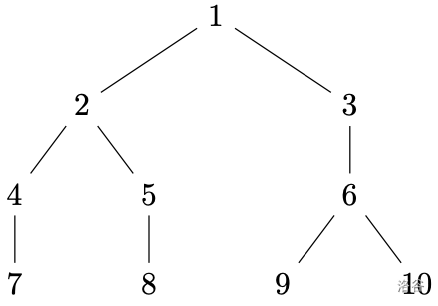
它由 a=(1,2,6) 参数化而来。
第 i 层包含节点 2i(i−1)+1,⋯,2i(i+1)。节点 ai 有两个孩子,而其他同层的节点都只有一个孩子。
请回答 q 个询问,求 x,y 的最大公共祖先,即既是 x 的祖先,又是 y 的祖先且权值最大的节点。
输入格式
第一行包含三个整数 n,q,t,分别表示参数的数量、询问次数和用来决定节点权值的参数。
第二行输入一个长度为 n 的序列 a(其中对于每一个数 ai 有 2i(i−1)<ai≤2i(i+1))。
接下来的 q 行中的第 i 行包含两个整数 x~i 和 y~i($1 \le \tilde x_i, \tilde y_i \le \frac{(n+1)(n+2)}{2}$),用来决定询问时节点的权值。
设 zi 为第 i 次询问的结果,规定 z0=0。第 i 次询问的权值为:
$$x_i=[(\tilde x_i-1+t \times z_{i-1}) \bmod \frac{(n+1)(n+2)}{2}]+1
$$$$x_i=[(\tilde y_i-1+t \times z_{i-1}) \bmod \frac{(n+1)(n+2)}{2}]+1
$$
注:当参数 t=0 时,满足 xi=x~i,yi=y~i。当 t=1 时,权值应通过先前的答案来决定。
输出格式
输出共 q 行,其中第 i 行,输出 xi 和 yi 的最大公共祖先。
3 5 0
1 2 6
7 10
8 5
6 2
9 10
2 3
1
5
1
6
1
3 5 1
1 2 6
7 10
8 5
6 2
9 10
2 3
1
6
2
1
1
提示
【样例解释 #1 / #2】
两个样例所表示的树的形状在题目描述的图中已经呈现。
第二个样例中各个节点的权值:
x1=7,y1=10;
x2=9,y2=6;
x3=2,y3=8;
x4=1,y4=2;
x5=3,y5=4。
【数据范围】
| Subtask |
分值 |
数据范围及约定 |
| 1 |
10 |
q=1,t=0 |
| 2 |
n≤1000,t=0 |
| 3 |
30 |
t=0 |
| 4 |
60 |
t=1 |
对于 100% 的数据,1≤n,q≤2×105,t∈{0,1}。
【说明】
本题分值按 COCI 原题设置,满分 110。
题目译自 COCI2020-2021 CONTEST #4 T5 Specijacija。

