题目描述

This is the $20-th$ Northeastern European Regional Contest $(NEERC).$ Cactus problems had become a NEERC tradition. The first Cactus problem was given in $2005$ , so there is a jubilee -- $10$ years of Cactus.

Cactus is a connected undirected graph in which every edge lies on at most one simple cycle. Intuitively cactus is a generalization of a tree where some cycles are allowed. Multiedges (multiple edges between a pair of vertices) and loops (edges that connect a vertex to itself) are not allowed in a cactus.

You are given a cactus. Let's move an edge -- remove one of graph's edges, but connect a different pair of vertices with an edge, so that a graph still remains a cactus. How many ways are there to perform such a move?

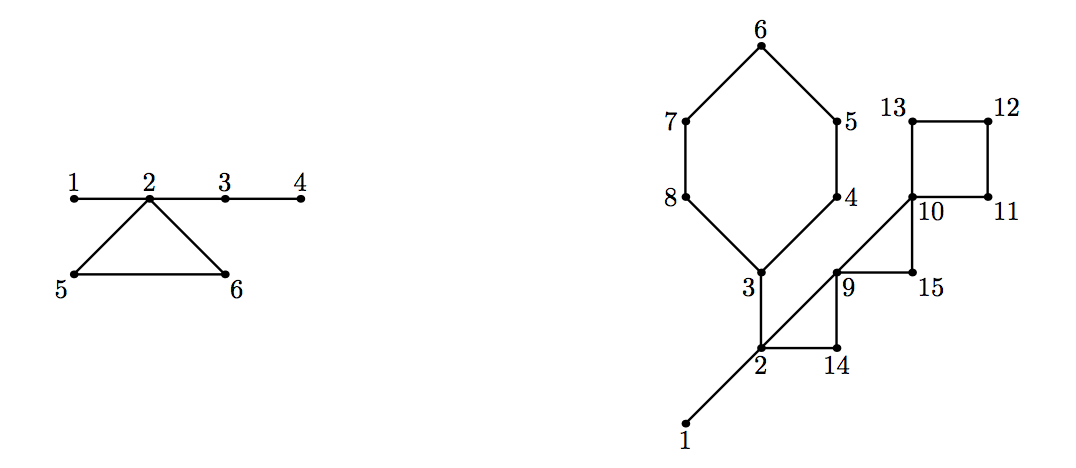
For example, in the left cactus above (given in the first sample), there are $42$ ways to perform an edge move. In the right cactus (given in the second sample), which is the classical NEERC cactus since the original problem in $2005$ , there are $216$ ways to perform a move.

输入格式

The first line of the input file contains two integers $n$ and $m (1 \le n \le 50 000 , 0 \le m \le 50 000)$ . Here $n$ is the number of vertices in the graph. Vertices are numbered from $1$ to $n$ . Edges of the graph are represented by a set of edge-distinct paths, where $m$ is the number of such paths.

Each of the following $m$ lines contains a path in the graph. A path starts with an integer $k_{i} (2 \le k_{i} \le 1000)$ followed by $k_{i}$ integers from $1$ to $n$ . These $k_{i}$ integers represent vertices of a path. Adjacent vertices in a path are distinct. Path can go to the same vertex multiple times, but every edge is traversed exactly once in the whole input file.

The graph in the input file is a cactus.

输出格式

Write to the output file a single integer -- the number of ways to move an edge in the cactus.

题目大意

题目描述

定义一种无向连通图叫仙人掌图（Cactus图）。仙人掌图中没有重边和自环，并且其中的每一条边至多位于一个简单环上。简单地说，仙人掌图是树的一种泛化形式，其中允许出现一些环。

现在有一个仙人掌图，你每次可以移动一条边（移除图的一条边，并将另一对顶点用一条边连接起来）。问如果要让后来得到的新图仍然是仙人掌图，有多少种移动边的办法？

输入格式

第一行包含两个整数n和m，分别表示图中的顶点数（顶点的编号分别为${1,2,3,...,n}$）和边的数目，且满足

$$1≤n≤50000,0≤m≤50000$$

第2~m+1行，每一行表示一条路径（从一个顶点出发一直往后走，直到当前所在的顶点没有任何未走过一条边）。

（译者注：虽然应该都能看出来了，但是还是用一个递归函数更浅显易懂）

设路径的开始点为$q_1$，$E_i$表示第$i$个点的边,$vis$数组中存储已经走过了的边，则整条路径可定义为：

1.x←q1
2.f(x)
	1.add(vis[],x)
	2.for i∈Ex do
	1.if i not in vis[] then
		1.call f(i->to)
3.print(vis[])

即：每一行的开始有一个整数$k_i$，满足 $2≤k_i≤1000$，紧接着有$k_i$个整数，表示这条路径所经过的顶点$q_i$，满足$q_i∈[1,n]$。

数据保证路径中的相邻顶点是不同的。

在路径中可以多次到达同一个顶点，但在整个输入文件中，每条边只遍历一次。

数据保证输入文件中的图形是仙人掌。

输出格式

输出文件中只有一个整数，即移动仙人掌图中一条边的方法数。

数据范围

$$1≤n≤50000,0≤m≤50000,2≤k_i≤1000,q_i∈[1,n]$$

6 1
7 1 2 5 6 2 3 4

42

15 3
9 1 2 3 4 5 6 7 8 3
7 2 9 10 11 12 13 10
5 2 14 9 15 10

216

提示

Time limit: 1 s, Memory limit: 256 MB.