题目描述

Warning for C++ users: The large size of integers involved in this problem may require the use of the long long data type instead of the int data type.

Shor the Duck is playing a game with his friends! The game is played on a 1-dimensional grid consisting of $n$ cells in, arranged in a row and numbered from $1$ to $n$ from left to right.

Each cell has a button. The button on cell $i$ will be permanently pressed if at any point in time there are at least $a[i]$ ducks on that cell. Even if the ducks leave, the button remains pressed. To win the game, all $n$ buttons must be pressed.

Initially, there are $d$ ducks on cell $1$. In one move, a single duck can move one cell left or right.

Determine the minimum total number of moves required to win the game. It is guaranteed that it is possible to win the game with some number of moves.

输入格式

Your program must read from standard input.

The first line of input contains two space-separated integers $n$ and $d$.

The second line of input contains $n$ space-separated integers $a[1], a[2], \ldots, a[n]$.

输出格式

Your program must print to standard output.

Output a single integer, the minimum total number of moves required to win the game.

2 199
175 42

42

5 3
1 1 0 1 0

3

5 7
2 2 2 2 2

8

7 5
1 3 3 4 5 5 5

30

8 9
7 6 6 6 3 3 3 1

28

8 5
2 3 5 1 4 2 1 0

21

4 1000000000
1 1 1 999999999

2999999997

提示

Subtasks

For all test cases, the input will satisfy the following bounds:

• $1 \leq n \leq 200\,000$
• $1 \leq d \leq 10^9$
• $0 \leq a[i] \leq d$ for all $1 \leq i \leq n$
• It is possible to win the game with some number of moves.

Your program will be tested on input instances that satisfy the following restrictions:

Subtask	Marks	Additional Constraints
$0$		Sample test cases
$1$	$8$	$n = 2$
$2$	$5$	$a[i] = 0$
$3$	$11$	$a[i] \leq 1$
$4$	$6$	All values of $a[i]$ are equal
$5$	$19$	$n, d \leq 1000$
$6$	$12$	$a[i]$ is non-decreasing
$7$	$16$	$a[i]$ is non-increasing
$8$	$23$	No additional constraints

Sample Test Case 1 Explanation

This test case is valid for subtasks $1, 5, 7$, and $8$.

Sample Test Case 2 Explanation

This test case is valid for subtasks $3, 5$, and $8$.

Sample Test Case 3 Explanation

This test case is valid for subtasks $4, 5, 6, 7$, and $8$.

Sample Test Case 4 Explanation

This test case is valid for subtasks $5, 6$, and $8$.

Sample Test Case 5 Explanation

This test case is valid for subtasks $5, 7$, and $8$.

Sample Test Case 6 Explanation

This test case is valid for subtasks $5$ and $8$.

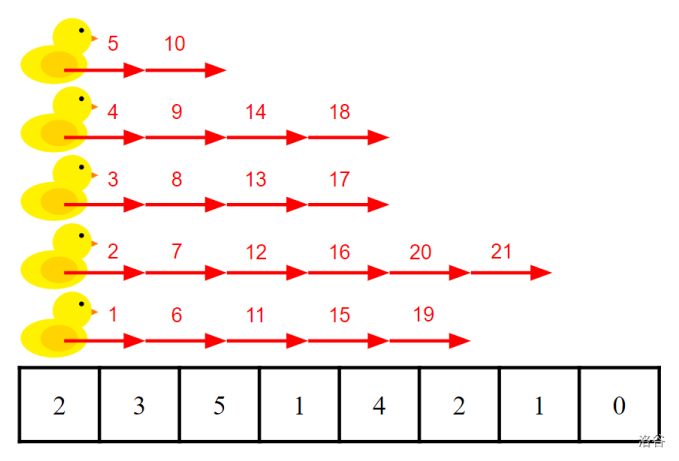
One possible sequence of moves that minimises the total number of moves is shown above. Each red arrow is a move, and the number above it indicates the order of the moves, with move $1$ coming first.

• Button $1$ is first pressed before any moves occur.
• Button $2$ is first pressed after move $3$.
• Button $3$ is first pressed after move $10$.
• Button $4$ is first pressed after move $11$.
• Button $5$ is first pressed after move $18$.
• Button $6$ is first pressed after move $20$.
• Button $7$ is first pressed after move $21$.
• Button $8$ is first pressed before any moves occur (since $a[8] = 0$).

Since all buttons are pressed by the end of all $21$ moves, $21$ moves is sufficient to win the game. It can be proven that $21$ moves is the minimum total number of moves needed.

Sample Test Case 7 Explanation

This test case is valid for subtasks $4, 6$, and $8$.