题目描述

给定正整数 $n,k$，请在一个 $n\times n$ 的网格中将 $kn$ 个方格染成黑色，其余方格染成白色，满足：

• 在水平或竖直方向上不存在连续的三个同色格。具体地：

  1. 不存在 $1\le i\le n,1\le j \le n-2$ 满足坐标为 $(i,j),(i,j+1),(i,j+2)$ 的格子均为黑色或均为白色。
  2. 不存在 $1\le i\le n-2,1\le j \le n$ 满足坐标为 $(i,j),(i+1,j),(i+2,j)$ 的格子均为黑色或均为白色。

• 每列中有恰好 $k$ 个黑色格。

• 对于任意 $i=1,2,\dots,k$，任意相邻的两列中从上至下第 $i$ 个黑色格的行坐标之差不超过 $1$。具体地，记第 $j$ 列的黑色格的坐标分别为 $(x_{1,j},j),(x_{2,j},j),\dots,(x_{k,j},j)$，其中 $x_{1,j}<x_{2,j}<\dots<x_{k,j}$，那么对于 $1\le i\le k,1\le j< m$ 有 $|x_{i,j}-x_{i,j+1}|\le 1$。

给出一种合法的方案，或判定无解。

输入格式

第一行包含一个正整数 $T$ $(1\le T\le 500)$，表示数据组数。

每组数据包含一行两个正整数 $n,k$ $(4\le n \le 1000,1\le k \le n)$，分别表示网格的大小与每列中黑色格的数量。

保证单个测试点中所有数据 $n^2$ 的和不超过 $10^6$。

输出格式

对于每组测试数据：

• 若不存在合法的染色方案，则仅输出一行一个字符串 No；
• 否则，先输出一行一个字符串 Yes，然后接下来 $n$ 行每行输出一个长度为 $n$，仅包含字符 # 与 . 的字符串，代表你染色方案中从上到下每一行的染色情况，其中字符 # 代表对应格染为黑色，字符 . 代表对应格染为白色。如果有多种合法的染色方案，输出任意一种即可。

3
4 2
6 1
9 5

Yes
#..#
.##.
.##.
#..#
No
Yes
.#.#..##.
#.#.##..#
#.##..##.
.#..##.##
#..##.#.#
.##..#.#.
##.##.#.#
#.##.##..
.##.##.##

提示

样例 #1 解释

对于第一组数据，以下为若干不符合条件的示例：

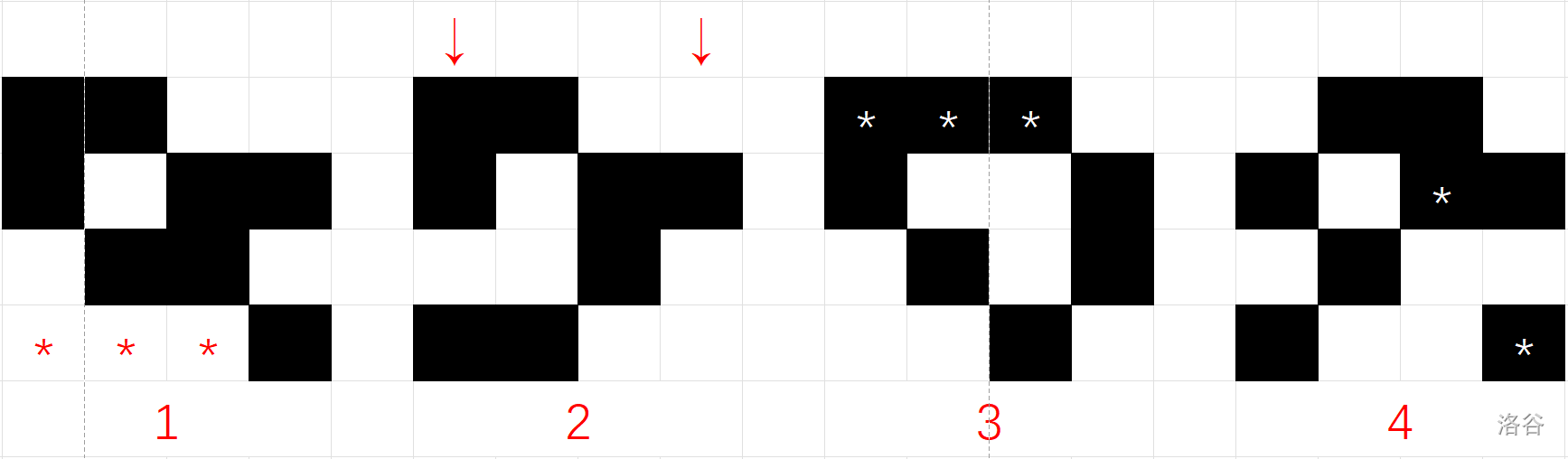
示例 $1$ 中左下角有连续的三个白色格，示例 $2$ 中第一列与第四列黑色格数量不正确，示例 $3$ 中左上角有连续的三个黑色格，示例 $4$ 中第三、四列的第二个黑色格行坐标之差大于 $1$。

对于第二组数据，容易发现不存在合法的染色方案。

对于第三组数据，下图中不同方位的黑色格用不同颜色标注后易见答案的合法性：

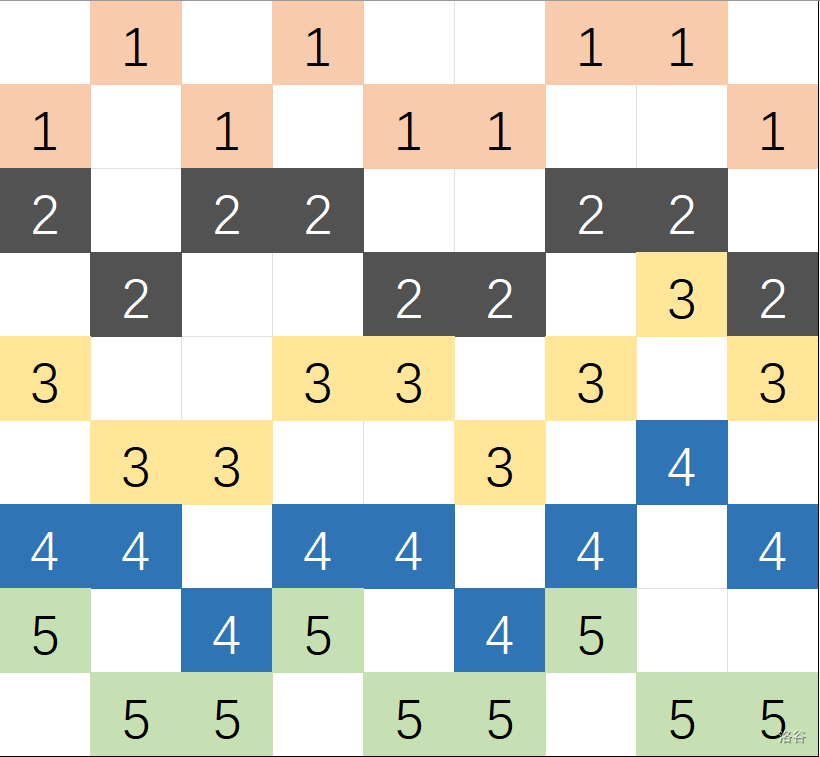
来源与致谢

来自 THUPC2025（2025 年清华大学学生程序设计竞赛暨高校邀请赛）决赛。感谢 THUSAA 的提供的题目。

数据、题面、标程、题解等请参阅 THUPC 官方仓库 https://thusaac.com/public。