题目背景
I came. I saw. I had anxiety. I left.
题目描述
给定一棵拥有 2n−1 个节点的二叉树,节点 i 的权值为 wi,节点 1 为根节点。对于所有非根节点 i 都有一条双向边连接节点 i 和节点 ⌊2i⌋。请注意 ⌊X⌋ 表示不大于 X 的最大整数。
定义节点 u,v 的距离为从节点 u 到节点 v 最少需要经过的边数。给定 m 组询问,第 i 组询问给定三个正整数 xi,yi,ki,你需要输出树上与 xi,yi 两个节点的距离都不超过 ki 的节点的权值之和。
输入格式
第一行输入两个正整数 n,m。
第二行输入 2n−1 个正整数,第 i 个正整数为 wi。
接下来 m 行,第 i 行输入三个正整数 xi,yi,ki。
输出格式
输出 m 行,每行一个整数,第 i 行的整数表示第 i 组询问的答案。
3 3
1 1 1 1 1 1 1
3 4 2
5 4 6
3 2 2
2
7
3
4 5
3 4 10 7 1 6 10 6 16 5 3 16 6 2 9
1 4 6
4 2 1
1 14 5
6 13 3
11 15 2
104
11
74
51
0
提示
「样例解释 #1」
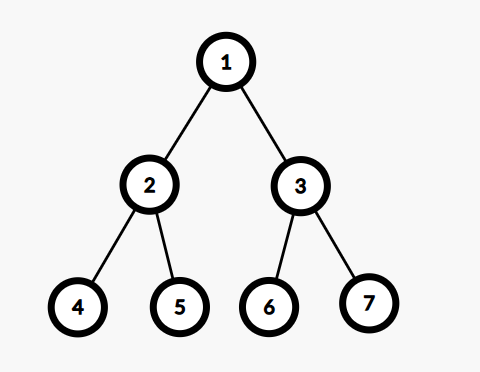
对于第一组询问,满足条件的节点有 1,2,权值和为 2。
对于第二组询问,满足条件的节点有 1,2,3,4,5,6,7,权值和为 7。
对于第三组询问,满足条件的节点有 1,2,3,权值和为 3。
「数据范围」
| 测试点编号 |
n≤ |
m≤ |
ki≤ |
wi≤ |
| 1 |
2 |
5 |
10 |
| 2∼3 |
10 |
1000 |
| 4∼5 |
18 |
2×105 |
5 |
109 |
| 6∼7 |
109 |
1 |
| 8∼10 |
109 |
对于 100% 的数据,2≤n≤18,1≤m≤2×105,1≤xi,yi≤2n−1,1≤ki≤109,1≤wi≤109,xi=yi。节点的编号是从 1 到 2n−1 的整数。

