luogu#P10610. 异界之门
异界之门
题目背景
跟随着线索,莲子来到了七夕坂。无暇欣赏此处的风景,高速运转着大脑的莲子,不断寻找异界的线索。翻转的地藏、奇异的裂缝、被隐匿的第五个季节……这个禁忌之中的世界,正向她揭晓着自己的秘密。
但莲子第一时间看到的只有梅莉,来不及思考,她一把抓住了梅莉的手——
题目描述
嗅觉敏锐的莲子察觉到,进入异界的方法一定和这些特别的地藏有所联系。她发现它们恰好构成了一棵形状特殊的树。
给定一棵 个点的带点权的有根树,其根为 ,且点 的点权为 。其满足对于任意两个深度相同的结点,它们的儿子数也相同。
为了进入异界,莲子进行了一些操作来改变这棵树的点权:
- 选择一条边,假设它连接了两点 ,设其中深度更高者为 (即 是 的儿子),将 加上 。
- 上述操作可以被执行任意多次,但是不能重复选择同一条边。
经过操作后,莲子求出了树的某个 DFS 序列,并记录下了这个 DFS 序列所对应的点权序列 (具体来说, 为 DFS 序过程中遍历到的第 个点的点权)。
不幸的是,她突然忘记了她进行过哪些操作,也忘记了如何 DFS 这棵树,她希望你能还原出任意一组合法的操作方案与 DFS 序列。
输入格式
第一行一个整数 。
对于接下来 行:第 行两个整数 ,其中 代表点 的父节点(特别的,,对于其余节点有 ), 代表点 的权值。
接下来一行 个整数描述序列 ,代表莲子的 DFS 序列所对应的点权序列 。保证一定存在一种合法的操作方式和操作后的 DFS 方式得到序列 。
输出格式
第一行一个整数 ,表示你进行的操作数。
接下来一行 个数,第 个数 代表你在第 次操作选择连接节点 和其父节点 的边进行操作。
接下来一行 个数描述一个排列 ,其中 代表你构造的 DFS 序列中遍历到的第 个节点为点 。
4
0 1
1 2
2 3
3 4
1 3 5 9
3
3 4 2
1 2 3 4
5
0 1
1 -1
1 -1
2 3
3 4
1 0 3 0 3
3
2 5 3
1 2 4 3 5
4
0 1
1 2
1 3
1 4
1 4 3 3
1
2
1 4 2 3
5
0 1
1 1
1 1
2 1
3 1
1 2 2 2 3
4
2 4 5 3
1 3 5 2 4
提示
样例解释
样例 #1
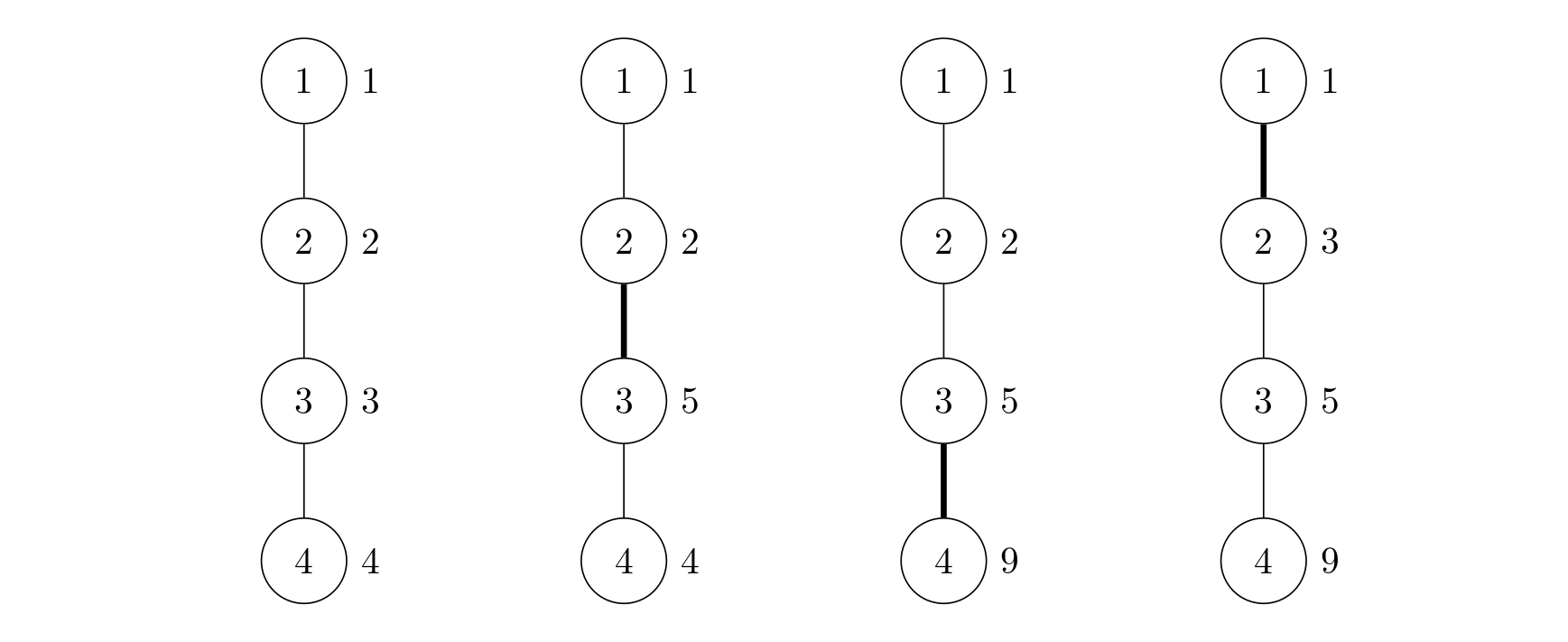
其中一种可行的方案是依次操作边 ,操作后的树的点权序列为 ,选出的 DFS 序列为 。
注意到该样例符合特殊性质 。
样例 #2
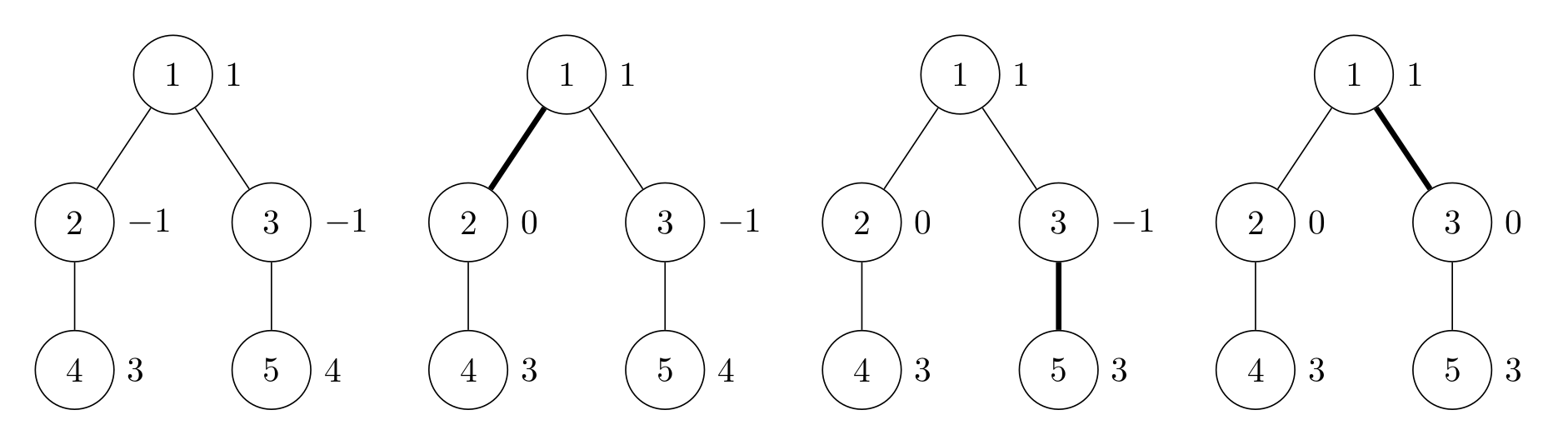
其中一种可行的方案是依次操作边 ,操作后的树的点权序列为 ,选出的 DFS 序列为 。
样例 #3

其中一种可行的方案是依次操作边 ,操作后的树的点权序列为 ,选出的 DFS 序列为 。
注意到该样例符合特殊性质 。
样例 #4
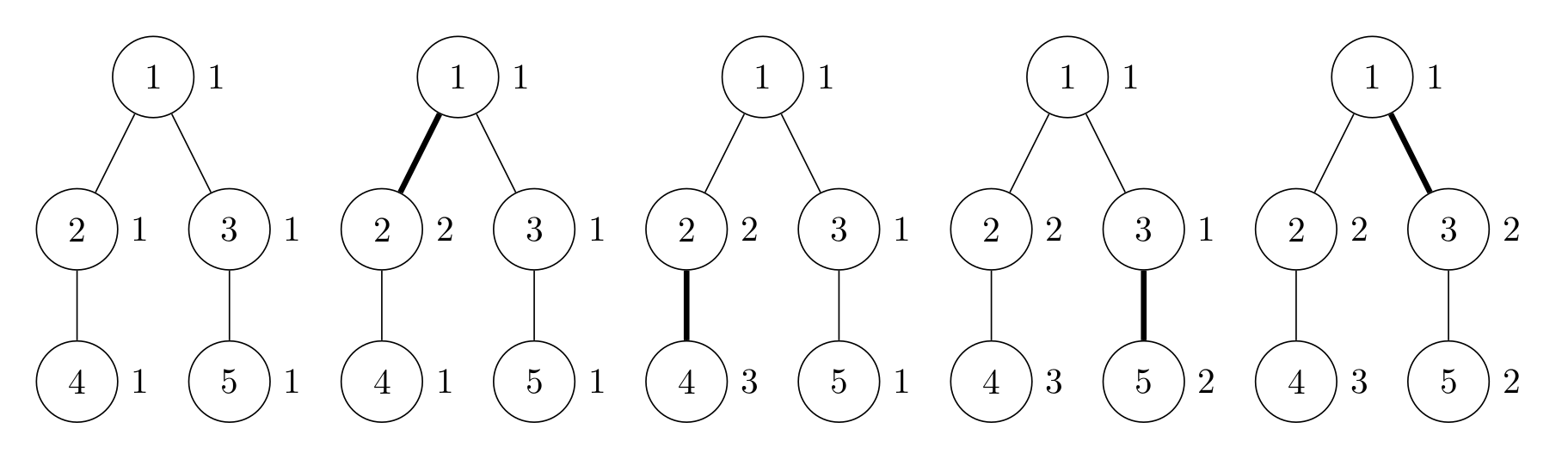
其中一种可行的方案是依次操作边 ,操作后的树的点权序列为 ,选出的 DFS 序列为 。
注意到该样例符合特殊性质 。
数据范围
本题采用捆绑测试。
$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|}\hline \textbf{Subtask} & \textbf{\textsf{分值}} & \bm{n\le } & \textbf{\textsf{特殊性质}}&\textbf{Subtask \textsf{依赖}}\cr\hline 1 & 10 & 6 & - &-\cr\hline 2 & 10 & 100 & \mathbf{A}&- \cr\hline 3 & 10 & 100 & \mathbf{B}&- \cr\hline 4 & 15 & 2\times 10^3 & \mathbf{C}&- \cr\hline 5 & 15 & 2\times 10^3 & \mathbf{D}&- \cr\hline 6 & 15 & 100 & -&1,2,3 \cr\hline 7 & 25 & 2\times 10^3 & -&1,2,3,4,5,6 \cr\hline \end{array} $$特殊性质 :保证给出的树满足 ()。
特殊性质 :保证给出的树满足 ()。
特殊性质 :保证给出的树满足 。
特殊性质 :保证给出的树满足所有非叶节点儿子数不超过 。
对于所有数据满足:,,。
