题目描述

题目译自 Romanian Master of Informatics 2021 Day2 T2 「Paths」

橘猫找到了一个有 $N$ 个顶点（编号从 $1$ 到 $N$）的树。在连接顶点 $x_{i}$ 和 $y_{i}$ 的每条边 $i\ (1 \leq i<N)$ 上，都有 $c_{i}$ 个特殊的猫零食。

橘猫可以选择恰好 $K$ 个顶点，从树的根节点走到每个选择的顶点，沿着从根节点到相应顶点的路径，并沿途取走所有的猫零食。当然，他只能在每条边上取一次零食。因为橘猫是一只好奇的猫，他想知道对于 $1$ 到 $N$ 的每个 $i$，如果根节点是顶点 $i$，他通过优化选择 $K$ 个顶点可以获得的最大可能的零食数量，。

输入格式

输入的第一行包含两个整数 $N$ 和 $K$，分别是树的顶点数和橘猫将选择的顶点数。接下来的 $N-1$ 行，每行包含三个整数 $x_{i}$、$y_{i}$ 和 $c_{i}$，描述树的边。

输出格式

输出 $N$ 行，第 $i$ 行输出如果树的根节点是顶点 $i$，橘猫可以获得的最大零食数量。

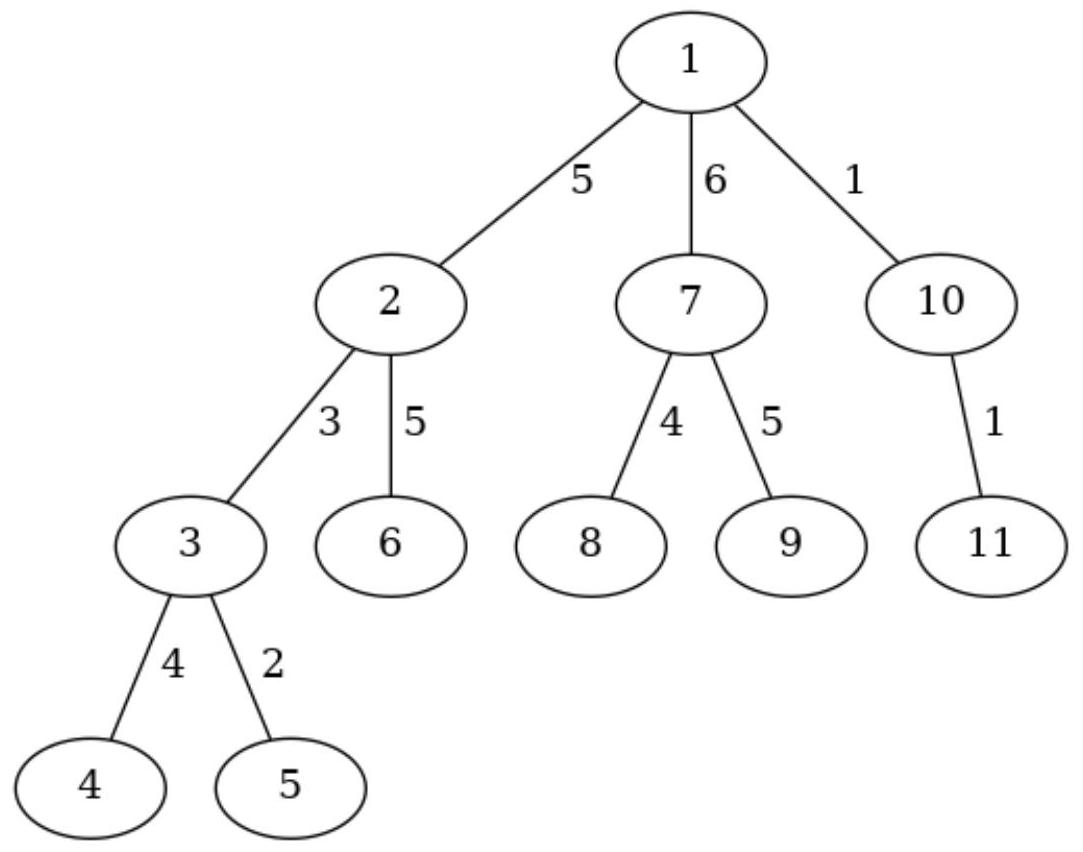
11 3
1 2 5
2 3 3
2 6 5
3 4 4
3 5 2
1 7 6
7 8 4
7 9 5
1 10 1
10 11 1

28
28
28
32
30
32
28
32
32
29
30

如果根节点是顶点 $1$，那么橘猫可以选择顶点 $4,6,9$。从根节点到所选顶点的路径是 $1\to 2\to 3\to 4,1\to 2\to 6,1\to 7\to 9$，沿这些路径的零食数量是 $5+3+4+5+6+5=28$。请注意，边 $1\to 2$ 上的零食只计算一次。

数据范围与提示

对于所有输入数据，满足：

• $1 \leq K \leq N \leq 10^5$
• $0 \leq c_{i} \leq 10^9\ (1 \leq i<N)$

详细子任务附加限制及分值如下表所示。