atcoder#ASAPORO2F. Unicyclic Graph Counting
Unicyclic Graph Counting
题目描述
すぬけくんは以下のような問題を考えました。
長さ の数列 が与えられます。 以下の条件を満たす頂点に のラベルがついた 頂点の無向グラフの数を modulo で求めてください。
- グラフは単純かつ連結
- 頂点 の次数は
$ 2\ \leq\ N,\ 1\ \leq\ d_i\ \leq\ N-1,\ {\rm\ Σ}\ d_i\ =\ 2(N-1) $ を満たす場合 には、この問題の答えは $ \frac{(N-2)!}{(d_{1}\ -1)!(d_{2}\ -\ 1)!\ ...\ (d_{N}-1)!} $ で表せることが証明できます。
すぬけくんは $ 3\ \leq\ N,\ 1\ \leq\ d_i\ \leq\ N-1,\ {\ \rm\ Σ}\ d_i\ =\ 2N $ を満たす場合 どうなるかが気になっています。 すぬけくんの代わりにこの問題を解いてください。
输入格式
入力は以下の形式で標準入力から与えられる。
输出格式
答えを出力せよ。
题目大意
题目大意
求有多少个点的环套树,满足第个点的度数为给定的。答案对取模。
环套树是一个个点、条边的简单(无重边、无自环)联通无向图。
输入格式
第一行一个正整数,表示点的个数。
第二行有个整数,表示每个点的度数。
输出格式
输出仅一行一个整数为答案,答案对取模。
数据范围
翻译提供者:浮尘ii
5
1 2 2 3 2
6
16
2 1 3 1 2 1 4 1 1 2 1 1 3 2 4 3
555275958
提示
制約
部分点
- 点分のデータセットでは が成立する
- 別の 点分のデータセットでは が成立する
- 別の 点分のデータセットでは が成立する
Sample Explanation 1
- 以下の図に示されるような 通りです 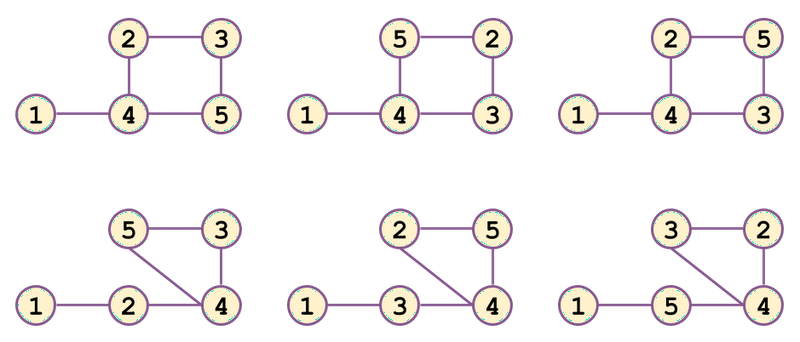
Sample Explanation 2
- で割ったあまりを求めてください
