题目描述
縦 H マス横 W マスのグリッドがあります。グリッドの上から i 行目、左から j 列目のマスを (i, j) と呼びます。
グリッドの各マスには # と . のいずれかの文字が書かれています。(i, j) に書かれている文字を C[i][j] とします。また、整数 i, j が 1 ≤ i ≤ H と 1 ≤ j ≤ W の少なくとも一方を満たさない場合、 C[i][j] を . と定義します。
正整数 a, b, n が以下の条件を全て満たす時、(a,b) および (a+d,b+d),(a+d,b−d),(a−d,b+d),(a−d,b−d) (1 ≤ d ≤ n) の 4n + 1 マスを (a,b) を中心とするサイズ n のバツ印 と呼びます。
- C[a][b] は
# である。
- 1 ≤ d ≤ n を満たす整数 d について、 C[a+d][b+d],C[a+d][b−d],C[a−d][b+d],C[a−d][b−d] はいずれも
# である。
- $C[a+n+1][b+n+1],C[a+n+1][b-n-1],C[a-n-1][b+n+1],C[a-n-1][b-n-1]$ のうち少なくとも 1 つは
. である。
例えば次の図で示された例では、(2, 2) を中心とするサイズ 1 のバツ印と (3, 7) を中心とするサイズ 2 のバツ印がグリッド上にあります。

グリッドにはいくつかのバツ印があります。バツ印を構成するマス以外に # は書かれていません。
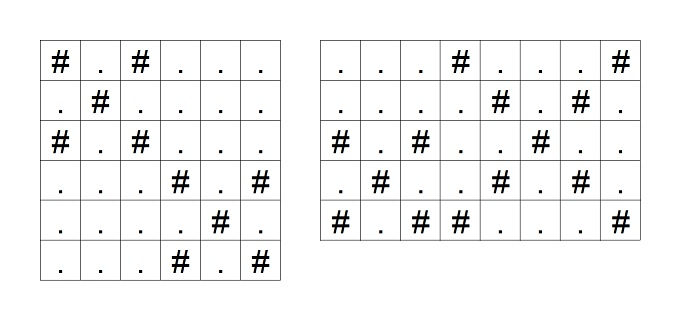
また、異なるバツ印を構成するマス同士は頂点を共有しません。以下の 2 つのグリッドは異なるバツ印を構成するマス同士が頂点を共有している例で、このようなグリッドの状態は入力として与えられません。 例えば左のグリッドでは (3, 3) と (4, 4) が頂点を共有しているのが条件に反しています。
N = min(H, W) とします。また、サイズ n のバツ印の個数を Sn とします。S1, S2, …, SN を計算してください。
输入格式
入力は以下の形式で標準入力から与えられる。
H W C[1][1]C[1][2]… C[1][W] C[2][1]C[2][2]… C[2][W] ⋮ C[H][1]C[H][2]… C[H][W]
输出格式
S1, S2, …, SN を空白区切りで出力せよ。
题目大意
给定一个 H×W 的矩阵(只有 # 和 . 这两种字符,第 i 行第 j 列的元素记作 Ci,j),求其中由字符 # 组成的、大小为 i 的十字架个数(记作 Si)。
把 S1...min(H,W) 依次输出。
对大小为 x 的十字架的定义:
如果数对 (i,j) 满足以下条件,则称由 Ci,j,Ci−1,j−1,Ci−2,j−2,...Ci−x,j−x,
Ci−1,j+1,Ci−2,j+2,...Ci−x,j+x,
Ci+1,j−1,Ci+2,j−2,...Ci+x,j−x,
Ci+1,j+1,Ci+2,j+2,...Ci+x,j+x,
这 4x+1 个点组成的图形为大小为 x 的十字架(不同十字架之间不共享顶点)。
- Ci,j 是字符
#。
- 对于整数 d(1≤d≤x),
Ci+d,j+d,Ci+d,j−d,Ci−d,j+d,Ci−d,j−d 都是字符 #。
- $C_{i+x+1,j+x+1},C_{i+x+1,j-x-1},C_{i-x-1,j+x+1},C_{i-x-1,j-x-1}$ 至少有一个是
. 。
数据范围:3≤H,W≤100
5 9
#.#.#...#
.#...#.#.
#.#...#..
.....#.#.
....#...#
1 1 0 0 0
3 3
...
...
...
0 0 0
3 16
#.#.....#.#..#.#
.#.......#....#.
#.#.....#.#..#.#
3 0 0
15 20
#.#..#.............#
.#....#....#.#....#.
#.#....#....#....#..
........#..#.#..#...
#.....#..#.....#....
.#...#....#...#..#.#
..#.#......#.#....#.
...#........#....#.#
..#.#......#.#......
.#...#....#...#.....
#.....#..#.....#....
........#.......#...
#.#....#....#.#..#..
.#....#......#....#.
#.#..#......#.#....#
5 0 1 0 0 0 1 0 0 0 0 0 0 0 0
提示
制約
- 3 ≤ H, W ≤ 100
- C[i][j] は
# または .
- 異なるバツ印を構成するマス同士は頂点を共有しない
- H, W は整数
Sample Explanation 1
問題文に書かれた説明の通り、(2, 2) を中心とするサイズ 1 のバツ印と (3, 7) を中心とするサイズ 2 のバツ印が書かれています。
Sample Explanation 2
バツ印が 1 個も書かれていない場合もあります。


