1 条题解
-
-2
首先,我们从 开始,这一个子任务保证了 ,即起点与终点在一条直线上。
我们根据规则,走一步就得向其他方向走,那么最优方案即为这样子:
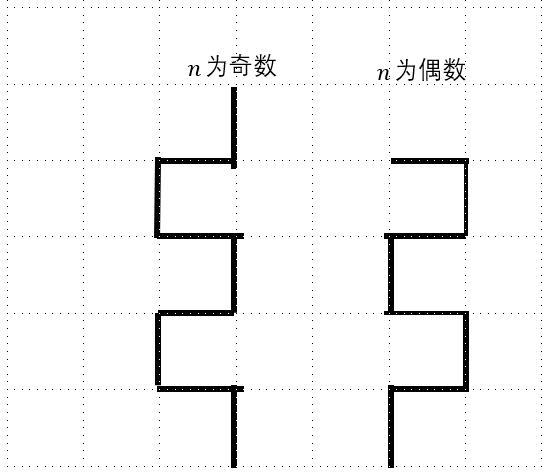
这样可能难以找到公式,那么我们转换一下即可。
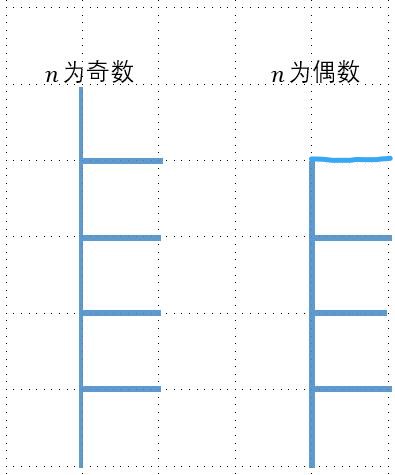
可以发现,如果起点与终点在一条直线上,那么 为奇数时就是要走 步,如果为偶数则要走 步。
接下来考虑扩展到所有数据,我们可以先走到与终点同一条直线上,那么图就是这样的。

右图经过了平移,发现,走到与终点同一条直线上要用的步数为 步,那么这个点与终点的距离就是 ,我们用 的思路做就行了。
考场 Code:
while(T--) { ans = 0; cin >> a >> b >> c >> d; x = llabs(c - a); y = llabs(d - b); t = llabs(x - y) + 1; //求出 N、M、n。N 表示为长边的长度,llabs 是我自己定义的一个用于 long long 的绝对值函数。 ans = min(x, y) * 2 - 1; //走到直线上 ans += t; if (t > 0) { if (t % 2 == 0) ans += t; else ans += (t - 1); } cout << ans << endl; }
- 1
信息
- ID
- 206
- 时间
- 2000ms
- 内存
- 512MiB
- 难度
- 4
- 标签
- (无)
- 递交数
- 139
- 已通过
- 61
- 上传者
