本题采用正难则反，正过来考虑如何统计答案较为复杂，则反过来统计当前词语有多少个集合会与其他词语重合，考虑当前为第一个词，且有N个1，不考虑与其他词语的重合集合，则有2^N -1个集合，再考虑重合，与第二个词重合的1的个数为X，则二者重合集合数为2^X -1个。与第三个词的重合的1的个数为Y，则重合数为2^Y -1,容斥定律知道多减去了三个单词都为1的部分组成的集合数，设三个词均为1的个数为cnt，则多减去了2^cnt -1，最后计算出当前单词的答案为2^N -1-2^X -1-2^Y -1+2^cnt -1=2^N- 2^X- 2^Y+ 2^ cnt,其他两个单词计算方式一样，最后三者取最小值即可。当然，这个时候，你会发现你仅仅得到40分，原因很简单，最后计算时需要取mod，你把取完mod后的答案进行比较，取了最小值对不对，不要小看我的情报网()。问题很明显，需要比较取模之前的三个数，那么问题来了，这么大的数怎么比较，难道要高精度比较吗，那很失败了。我这个时候想起了高中的比较方式，作差法。比如将第二个和第三个单词的答案作差，通过正负判断大小，得到ans2-ans3=(2^ (N2)+2^ Y)-(2^ (N3)+2^ X),然而现在答案还是不明显，但是从二进制的角度思考，(2^ (N2)+2^ Y)和(2^ (N3)+2^ X)，都是含有两个二进制位的数，根据二进制比较法，从高位到低位比较即可，换言之，谁最大的二进制位更小，那它的答案就更小，如果最大的二进制位一样，则比剩下的那一个就行。（当然有一个特例，比如N2=Y，导致二进制进位如何解决，不妨自己试试，模拟一下过程就知道上述的比较方法依然可行）。详细见程序的cmp函数，最终三个答案取最小即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mod=998244353,n;
char A[4][1145141];
int a[4][1145141];
ll qp(ll a,ll b){
	ll ans=1,base=a;
	while(b){
		if(b&1)ans=ans*base%mod;
		b>>=1;
		base=base*base%mod;
	}
	return ans;
}
ll x[4],cnt,X,Y,Z;
struct node{
	ll x1,y1;
	ll ans;
}fi[4];
bool cmp(node a,node b){
	if(max(a.x1,a.y1)==max(b.x1,b.y1)){
		return min(a.x1,a.y1)<min(b.x1,b.y1);
	}
	return max(a.x1,a.y1)<max(b.x1,b.y1);
}
int main() {
	cin>>n;
	for(int j=1;j<=3;j++){
		for(int i=1;i<=n;i++){
			cin>>A[j][i];
			a[j][i]=A[j][i]-'0';
			x[j]+=a[j][i];
		}
	}
	for(int i=1;i<=n;i++){
		if(a[1][i]&&a[2][i]&&a[3][i]){
			cnt++;
		}
		if(a[1][i]&&a[2][i]){
			X++;
		}
		if(a[1][i]&&a[3][i]){
			Y++;
		}
		if(a[2][i]&&a[3][i]){
			Z++;
		}
	}
	fi[1].x1=x[1];
	fi[1].y1=Z;
	fi[2].x1=x[2];
	fi[2].y1=Y;
	fi[3].x1=x[3];
	fi[3].y1=X;
	fi[1].ans=(qp(2,x[1])+qp(2,cnt)-qp(2,X)-qp(2,Y)+2*mod)%mod;
	fi[2].ans=(qp(2,x[2])+qp(2,cnt)-qp(2,X)-qp(2,Z)+2*mod)%mod;
	fi[3].ans=(qp(2,x[3])+qp(2,cnt)-qp(2,Z)-qp(2,Y)+2*mod)%mod;
	sort(fi+1,fi+3+1,cmp);
	cout<<fi[1].ans<<endl;
	return 0;
}

巧妙布局

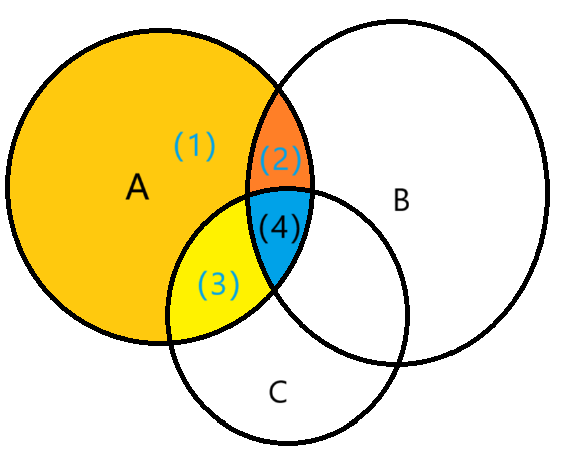
如果要计算词 $A$ 能够描述的轮数，要考虑四个部分，如上图。

若有（1）中元素，其他的可以任取。

若无（1）中元素，则：

• 必须有（2）（3）中元素。
• （4）中元素总是可以任取。

设大小分别为 $N_1,N_2,N_3,N_4$，则答案是

$$(2^{N_1}-1)\times 2^{N_2+N_3+N_4}+(2^{N_2}-1)(2^{N_3}-1)\times 2^{N_4} $$

比较三者能描述的轮数，取最小值。

时间复杂度是 $\Theta(n)$。

#include <bits/stdc++.h>
using namespace std;
using ll = long long int;

string intersection(string s, const string& t) {
	for(int i = 0; i < s.length(); i++) {
		if(t[i] != '1') s[i] = '0';
	}
	return s;
};

int compare(array<int, 4> x, array<int, 4> y) {
	int n = max(x[0], y[0]);
	vector<int> dif(n + 10, 0); 
	dif[x[0]] ++; dif[x[1]] --; dif[x[2]] --; dif[x[3]] ++;
	dif[y[0]] --; dif[y[1]] ++; dif[y[2]] ++; dif[x[3]] --;
	for(int i = 0; i < n; i++) {
		while(dif[i] < 0) dif[i + 1] --, dif[i] += 2;
		while(dif[i] >= 2) dif[i] -= 2, dif[i + 1] --;
	}
	for(int i = n + 5; i >= 0; i--) {
		if(dif[i] != 0) return dif[i]; // >0 : greater
	}
	return 0;
}

array<int, 4> min(array<int, 4> x, array<int, 4> y) {
	if(compare(x, y) >= 0) return y;
	return x;
}

void solve()
{
	int n; cin >> n;
	string s[3];
	cin >> s[0] >> s[1] >> s[2];
	vector<int> p(n + 2, 0); p[0] = 1;
	const int mod = 998244353;
	for(int i = 1; i <= n + 1; i++) p[i] = p[i - 1] * 2 % mod;
	
	array<int, 4> ans[3];
	
	for(int i = 0; i < 3; i++) {
		swap(s[0], s[i]);
		string AB = intersection(s[0], s[1]);
		string AC = intersection(s[0], s[2]);
		string ABC = intersection(AB, AC);
		int N4 = count(ABC.begin(), ABC.end(), '1'), N3 = count(AB.begin(), AB.end(), '1') - N4,
			N2 = count(AC.begin(), AC.end(), '1') - N4, N1 = count(s[0].begin(), s[0].end(), '1') - N2 - N3 - N4;
		
		// ans : 2^{N1+N2+N3+N4} - 2^{N2+N3+N4} + 2^{N2+N3+N4} - 2^N2 - 2^N3 + 2^N4
		// 2^{N1+N2+N3+N4} - 2^N2 - 2^N3 + 2^N4
		
		ans[i] = {N1 + N2 + N3 + N4, N2 + N4, N3 + N4, N4};
//		cout << s[0] << " " << N1 + N2 + N3 + N4 << " " << N2 + N4 << " " << N3 + N4 << " " << N4 << '\n';
	}
	
	array<int, 4> minv = min(min(ans[0], ans[1]), ans[2]);
	
	long long ret = 0; 
	ret += p[minv[0]];
	ret -= p[minv[1]];
	ret -= p[minv[2]];
	ret += p[minv[3]];
	ret = ((ret % mod) + mod) % mod;
	
	cout << ret << '\n';
}
int main()
{
	ios::sync_with_stdio(false); cin.tie(0);
//	int t; cin >> t; while(t--)
	solve();
	return 0;
}