1 条题解
-
0
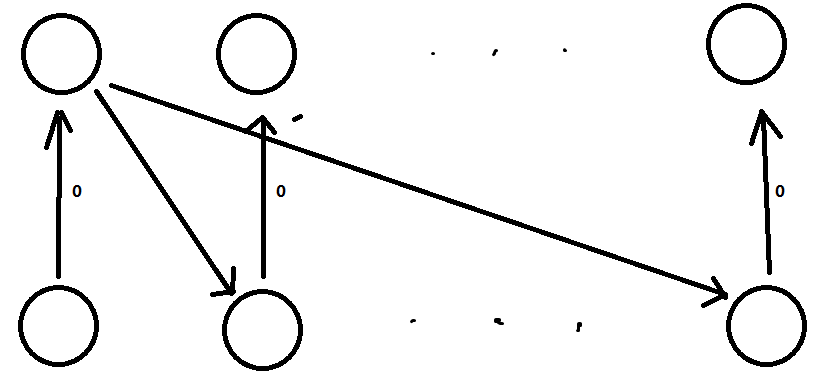
首先考虑有向边,把一个点拆成两个点,分别表示对应的 和 ,然后就 向 连边,然后 向 连一条为 的边。
就像下面这个图:
但会发现,这样的边数量依然是 条。
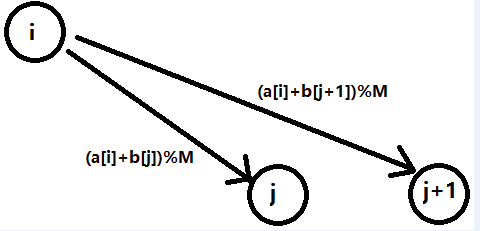
考虑先对 排序。
对于一个 ,找到一个 满足 最小,这个可以直接二分。
然后就会发现下面两种建边方式相同:
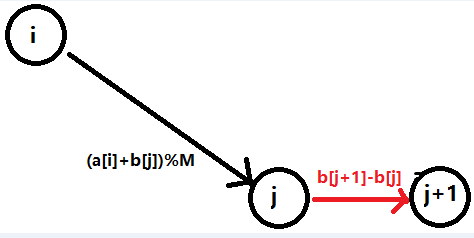
然后就会发现下面的红色边实际上都是相同的,因此直接下面的边建好,跑 dij 就好了。
代码
#include<bits/stdc++.h> #define mp make_pair #define eb emplace_back using namespace std; const int N=4e5+5; typedef pair<long long,int> pII; struct hzy{int x,y,id;}a[N]; vector<pair<int,int> > e[N]; priority_queue<pII,vector<pII>,greater<pII> > q; int vis[N],n,m; long long dis[N]; int low(int x){ if(a[n].y<x)return 1;//注意特判 int l=1,r=n; while(l+1<r){ int mi=l+r>>1; if(a[mi].y<x)l=mi; else r=mi; } if(a[l].y>=x)return l; return r; } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++)scanf("%d",&a[i].x); for(int i=1;i<=n;i++)scanf("%d",&a[i].y),a[i].id=i; sort(a+1,a+n+1,[](hzy a,hzy b){return a.y<b.y;}); for(int i=n+1;i<=2*n;i++)e[i].eb(i-n,0); for(int i=1;i<=n;i++){ int t=low(m-a[i].x);//找到和最小的那个 e[i].eb(n+t,(a[i].x+a[t].y)%m); } for(int i=1;i<n;i++)e[i+n].eb(n+i+1,a[i+1].y-a[i].y); e[n*2].eb(n+1,a[1].y+m-a[n].y); memset(dis,63,sizeof(dis)); for(int i=1;i<=n;i++)if(a[i].id==1){ dis[i]=0; q.push(mp(0,i)); } while(!q.empty()){ int x=q.top().second; q.pop(); if(vis[x])continue; vis[x]=1; for(auto i:e[x]){ int y=i.first,z=i.second; if(dis[y]>dis[x]+z){ dis[y]=dis[x]+z; q.push(mp(dis[y],y)); } } } for(int i=1;i<=n;i++)if(a[i].id==n)printf("%lld",dis[i]); }
- 1
信息
- ID
- 58
- 时间
- 1000ms
- 内存
- 256MiB
- 难度
- 10
- 标签
- 递交数
- 1
- 已通过
- 1
- 上传者