昨天上物理课，老师讲到人可通过声音传到两耳的时间差辨别声源的方位，然后我自已脑补了一个题目：

在平面直角坐标系中，已知点$A(x_{1},y_{1})$,$B(x_{2},y_{2})$,$P$到点$A$$、B$的距离分别为$s_{1},s{2}$且$s_{1}+s_{2}>\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}$,求点P的坐标。

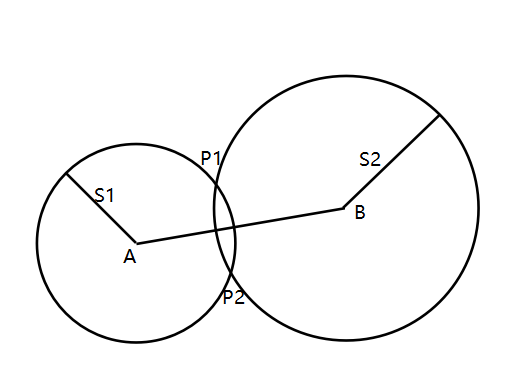
首先我们来思考一下：点$P$共有几个呢？这里需要用到圆的一个性质：圆心为O，半径为r的圆可以看成是所有到点O的距离等于r的点的集合，因此我们分别以点$A、B$为圆心，$s_{1},s_{2}$为半径画圆，两个圆分别为到点$A$距离为$s_{1}$和到点$B$距离为$s_{2}$的点的集合，那么这两个集合的交集即两圆的交点便是所求的点$P$。因为$s_{1}+s_{2}>\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}$，所以两圆相切，有两个交点，即点$P$有$2$个。

分别将这两个点记为$P_{1}$、$P_{2}$，我们先来研究$P_{1}$。

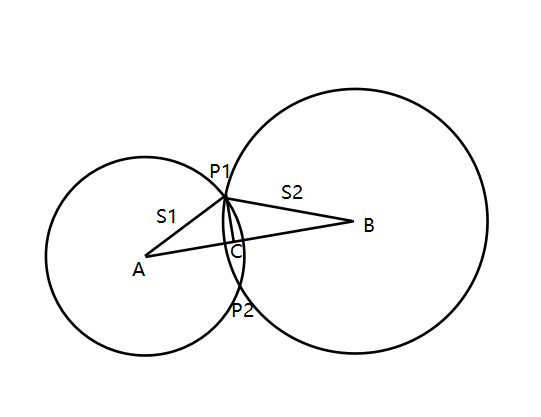
连接$AP_{1}$，$BP_{1}$，则$AP_{1}=s_{1}$，$BP_{1}=s_{2}$，又知$AB=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}$，那么就可以直接套用海伦公式:

记$a=s_{1},b=s_{2},c=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2},p=\frac{a+b+c}{2}$，则$S\triangle ABP_{1}=\sqrt{(p-a)(p-b)(p-c)}$.

过点$P_{1}$作$P_{1}C\bot AB$.

$\because AB=a,S\triangle ABP_{1}=\sqrt{(p-a)(p-b)(p-c)},P_{1}C\bot AB$

$\therefore P_{1}C=\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a}$

$\therefore AC=\sqrt{s_{1}^2-(\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a})^2}$（勾股定理）.

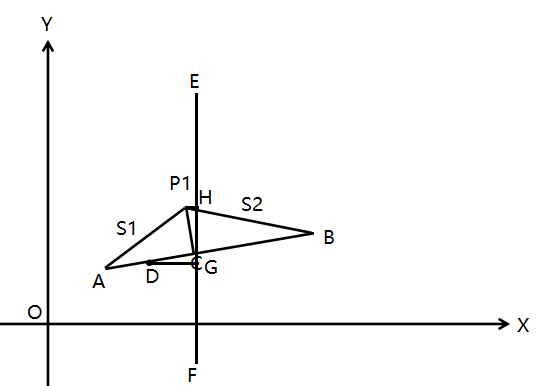
然后我们把$\triangle ABP_{1}$单独拎出来看看：

在$AC$上截取$DC=P_{1}C$，记点$C$的坐标为$(x_{3},y_{3})$，点$D$的坐标为$(x_{4},y_{4})$。将$\triangle ABP_{1}$置于平面直角坐标系中，过点$C$作$EF$平行于$y$轴，过点$D$作$DG\bot EF$，过点$P_{1}$作$P_{1}H\bot EF$。

$\because P_{1}C=\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a},DC=P_{1}C,AC=\sqrt{s_{1}^2-(\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a})^2}$

$\therefore AD=\sqrt{s_{1}^2-(\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a})^2}-\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a}$，将$AD$记为$s_{3}$.

由$AAS$或$ASA$可证得，$\triangle CP_{1}H\simeq\triangle DCG$，$\therefore CH=DG,P_{1}H=CG$.

$\therefore P_{1}(x_{3}-y_{3}+y_{4},y_{3}+x_{3}-x_{4})$.

至此，问题转化为了求点$C,D$的坐标。

如何求呢？我们知道一次函数的图像为一条直线，那么我们可以将$AB$看成一次函数.

设$AB$的解析式为$y=kx+b$，则有$\left\{\begin{aligned}kx_{1}+b=y_{1} \\kx_{2}+b=y_{2}\end{aligned}\right.$，解得$\left\{\begin{aligned}k=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \\b=\frac{x_{2}y_{1}+x_{1}y_{2}}{x_{2}-x_{1}}\end{aligned}\right.$，即$y=\frac{x(y_{2}-y_{1})}{x_{2}-x_{1}}+\frac{x_{2}y_{1}+x_{1}y_{2}}{x_{2}-x_{1}}=\frac{y_{1}(x_{2}-x)+y_{2}(x_{1}-x)}{x_{2}-x_{1}}$.这里因式子太长，姑且暂时记为$y=kx+b$.

设$x_{4}=x_{1}+temp_{1}$，则$y_{4}=y_{1}+k*temp_{1}$.

又$\because AD=s_{3}$

$\therefore s_{3}=\sqrt{temp_{1}^2+(k*temp_{1})^2}=\sqrt{temp_{1}^2(k^2+1)}$

$\therefore temp_{1}^2(k^2+1)=s_{3}^2$

$\therefore temp_{1}^2=\frac{s_{3}^2}{k^2+1}$

$\therefore temp_{1}=\sqrt{\frac{s_{3}^2}{k^2+1}}=\frac{s_{3}}{\sqrt{k^2+1}}=\frac{s_{3}*\sqrt{k^2+1}}{\sqrt{k^2+1}*\sqrt{k^2+1}}=\frac{s_{3}*\sqrt{k^2+1}}{k^2+1}$.

$\therefore x_{4}=x_{1}+\frac{s_{3}*\sqrt{k^2+1}}{k^2+1},y_{4}=y_{1}+\frac{k*s_{3}*\sqrt{k^2+1}}{k^2+1}$.

至此，我们求得了$x_{4}$和$y_{4}$，还需要求$x_{3},y_{3}$。

记$AC=s_{4},x_{3}=x_{1}+temp_{2}$，则有$y_{3}=y_{1}+k*temp_{2}$.

$\therefore s_{4}=\sqrt{temp_{2}^2+(k*temp_{2})^2}=\sqrt{temp_{2}^2(k^2+1)}$

$\therefore temp_{2}^2(k^2+1)=s_{4}^2$

$\therefore temp_{2}^2=\frac{s_{4}^2}{k^2+1}$

$\therefore temp_{2}=\sqrt{\frac{s_{4}^2}{k^2+1}}=\frac{s_{4}}{\sqrt{k^2+1}}=\frac{s_{4}*\sqrt{k^2+1}}{\sqrt{k^2+1}*\sqrt{k^2+1}}=\frac{s_{4}*\sqrt{k^2+1}}{k^2+1}$

$\therefore x_{3}=x_{1}+\frac{s_{4}*\sqrt{k^2+1}}{k^2+1},y_{3}=y_{1}+\frac{k*s_{4}*\sqrt{k^2+1}}{k^2+1}$

$\therefore P_{1}(x_{1}+\frac{\sqrt{k^2+1}(s_{4}-k*s_{4}+k*s_{3})}{k^2+1},y_{1}+\frac{\sqrt{k^2+1}(s_{4}+k*s_{4}-s_{3})}{k^2+1})$，其中$k=\frac{y_{2}-y_{1}}{x_{2}-x{1}}$，$s_{3}=\sqrt{s_{1}^2-(\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a})^2}-\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a}$，$s_{4}=\sqrt{s_{1}^2-(\frac{2\sqrt{(p-a)(p-c)(p-c)}}{a})}$，$a=s_{1}$，$b=s_{2}$，$c=\sqrt{(x_{1}-x{2})^2+(y_{1}-y_{2})^2}$，$p=\frac{a+b+c}{2}$.

同理可得，$P_{2}(x_{3}+y_{3}-y_{4},y_{3}-x_{3}+x_{4})$.

$\therefore P_{2}(x_{1}+\frac{\sqrt{k^2+1}(s_{4}+k*s_{4}-k*s_{3})}{k^2+1},y_{1}+\frac{\sqrt{k^2+1}(k*s_{4}-s_{4}+s_{3})}{k^2+1}) $，其中$k=\frac{y_{2}-y_{1}}{x_{2}-x{1}}$，$s_{3}=\sqrt{s_{1}^2-(\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a})^2}-\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a}$，$s_{4}=\sqrt{s_{1}^2-(\frac{2\sqrt{(p-a)(p-c)(p-c)}}{a})}$，$a=s_{1}$，$b=s_{2}$，$c=\sqrt{(x_{1}-x{2})^2+(y_{1}-y_{2})^2}$，$p=\frac{a+b+c}{2}$.

求完了！！！

然而似乎还有一步:

验证

根据图形，我们知道：当$s_{1}+s_{2}=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}$时，$P$点只有一个，即此时$P_{1},P_{2}$重合.

$\therefore k*s_{4}=k*s_{3},s_{4}=s_{3}$

$\therefore s_{4}=s_{3}$

$\therefore \sqrt{s_{1}^2-(\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a})^2}=\sqrt{s_{1}^2-(\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a})^2}-\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a}$

$\therefore \frac{2\sqrt{(p-a)(p-b)(p-c)}}{a}=0$

那么，$\frac{2\sqrt{(p-a)(p-b)(p-c)}}{a}$是否等于$0$呢？

$\because s_{1}+s_{2}=\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}$

$\therefore a+b=c$

又$\therefore p=\frac{a+b+c}{2}$

$\therefore p=\frac{c+c}{2}=c$

$\therefore p-c=0$

$\therefore \frac{2\sqrt{(p-a)(p-b)(p-c)}}{a}=0$

$\therefore s_{4}=s_{3}$

$\therefore$得证.

完结撒花！！！

$2023/9/16$完

下一篇：随笔#2023/9/17