• 不开long long见祖宗；

• 不写freopen见祖宗；

• 大数据处理取模取错见祖宗；

• 数组开小见祖宗；

• 内存超限见祖宗；

• 文件名打错见祖宗；

• 祖宗撸串去了，管不过来

练武不练功， 到老一场空。

10年Oi一场空， 不开long long 见祖宗。

刷题不会要答疑 答疑，debug找高爸

橙题307题

黄题59题

内积(点积)和外积(叉积)

UK

素数筛0

素数筛1

$ax^2+bx+c=0,x=\frac{-b\pm\sqrt{b^2-4ac}}{2a},\Delta=b^2-4ac且x_1+x_2=-\frac{b}{a},x_1*x_2=\frac{c}{a}$

$p为质数，a^{p-1}\bmod p=1,ax\bmod p=1,x=a^{p-2},设a_{1～p-1}为1～p-1\bmod p意义下的逆元,a_1=1,i\not=1,a_i=(p-\frac p i\times a_{p\bmod i}\bmod p$

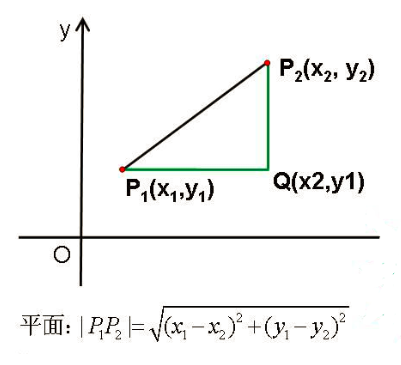
三维欧几里德距离($P_1$与$P_2$的距离)=$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

二维欧几里德距离($P_1$与$P_2$的距离)=$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

一维欧几里德距离($P_1$与$P_2$的距离)=$\sqrt{(x_1-x_2)^2}$

$均值不等式:\frac{a+b}{2}\geqslant\sqrt{ab}，其中a,b\geqslant0,\frac{a+b}{2}为a,b的算术平均值，\sqrt{ab}为几何平均值。$

设$2^n|a$，$2^n$的整除特征：$a~\bmod 10^n~\bmod2^n=0$

next_permutation用于求下一个字典序。

prev_permutation 用法:函数的两个参数为内存中的一段连续空间的起点和终点，每次调用都将指定内存中的值修改为上一个字典序，如果当前排列已是第一个，返回“false”。

$\color{#ff0}黄金\color{#f00}分割数:\frac{-1\plusmn\sqrt{5}}{2}$

三体

$\lim_{x\to\infty}(\frac{a}{(a+1)^1}+\frac{a}{(a+1)^2}+...\frac{a}{(a+1)^x})=1$ $利率=\frac{\frac{利息}{本金}}{时间}*100\%$

秦九韶公式（三角形）:$S=\frac{1}{2}\sqrt{a^2b^2-(\frac{a^2+b^2-c^2}{2})^2}$

秦九韶算法（求多项式）：$f(x)=a_nx^n+a_{n-1}x^{n-1}+...a_1x+a_0=(((...(a_nx+a_{n-1})x+a_{n-2})x...)))+a_0$

线性组合(V表示矢量)$aV_1+bV_2+cV_3+...=V$

秦九韶算法(大衍求一数)现代数学表达：$N=\sum{M_i}{x_i}{a_i}同余x\mod v \begin{Bmatrix}M_1x_1同余1\mod m_1 \\M_2x_2同余1\mod m_2\\\ M_3x_3同余1\mod m_3\\\\M_4x_4同余1\mod m_4 \end{Bmatrix}$

配方法:$ax^2+bx+c=0$

$ax^2+bx=c$

$ax^2+bx+(\frac{b}{2})^2=c+(\frac{b}{2})^2$

$(ax+\frac{b}{2})^2=c+(\frac{b}{2})^2$

$ax+\frac{b}{2}=c+\frac{b}{2}$

二次函数$y=ax^2+bx+c$可以通过配方化成$y=a(x-h)^2+k$的形似，即$y=a(x+\frac{b}{2a})^2+\frac{4ac-b^2}{2a}$.因此，抛物线的对称轴是$x=-\frac{b}{2a}$，顶点是$(-\frac{b}{2a},\frac{4ac-b^2}{4a})$.如果$a>0$,当$x<-\frac{b}{2a}$时，$y$随$x$的增大而减小，当$x>-\frac{b}{2a}$时,$y$随$x$的增大而增大(开口向上)；如果$a<0$,当$x<-\frac{b}{2a}$时，$y$随$x$的增大而增大，当$x>-\frac{b}{2a}$时,$y$随$x$的增大而减小（开口向下）.

圆周角=$\frac{1}{2}$圆心角。

两角和公式是：$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$(正弦两角和公式)，$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$(余弦两角和公式)，$\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}(\alpha,\beta,\alpha+\beta\not=k\pi+\frac{\pi}{2},k\isin Z)$(正切两角和公式)，$\cot(\alpha+\beta)=\frac{\cot\alpha\cot\beta-1}{\cot\beta+\cot\alpha}(\alpha,\beta,\alpha+\beta\not=k\pi,k\isin Z)$(余切两角和公式)，$\sec(\alpha+\beta)=\frac{\sec\alpha\cot\beta-1}{1-\tan\alpha\tan\beta}(\alpha,\beta,\alpha+\beta\not=k\pi+\frac{\pi}{2},k\isin Z)$(正割两角和公式)，$\csc(\alpha+\beta)=\frac{\csc\alpha\csc\beta}{1-\cot\alpha\cot\beta}(\alpha,\beta,\alpha+\beta\not=k\pi,k\isin Z)$(余割两角和公式)

三角函数的值：设直角三角形中一个锐角为$\alpha$，对边为$a$,斜边为$c$。正弦函数$(\sin)$：$\sin\alpha=\frac{a}{c}$。余弦函数$(\cos)$：$\cos\alpha=\frac{b}{c}$。正切函数$(\tan)$：$\tan\alpha=\frac{a}{b}(b\not=0)$。余切函数$(\cot)$：$\cot\alpha=\frac{b}{a}(a\not=0)$。正割函数$(\sec)$：$\sec\alpha=\frac{c}{b}(b\not=0)$。余割函数$(\csc)$：$\csc\alpha=\frac{c}{a}(a\not=0)$。

两直线垂直的乘积是$-1$。

平底锅模型：$y=\lvert x-a\rvert+\lvert x-b\rvert$

尖底锅模型：$y=\rvert x-a\lvert+\lvert x-b\rvert+\lvert x-c\rvert$

priority_queue<a,vector<a>,greater<a>>q;

是优先队列！！！

一次函数：

• 斜截式 ($Slope-Intercept Form$)：y = kx + b，其中 k 是斜率，b 是y 轴上的截距。
• 一般式 ($General Form$)：$Ax + By + C = 0$，其中 $A$，$B$ 不全为零。
• 两点确定直线方程：给定两点 $P1(x1, y1)$ 和 $P2(x2, y2)$ 且 $x1 = x2$, $y1 =y2$。$\frac{y-y_1}{y_2-y_1}=\frac{x-x_1}{x_2-x_1}$
• 斜率的几何意义：斜率 $k$ 表示直线相对于 $x$ 轴正方向的倾斜程度。$k=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$
• 斜率与倾斜角：倾斜角 $\alpha$ 是直线与 x 轴正向的夹角 $(0 \leqslant \alpha < \pi)$。$k=\tan \alpha$
• 点到直线的距离：点 $P(x0, y0)$ 到直线 $Ax + By + C = 0$ 的距离 $d$。$d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}}$
• 两条直线交点：联立两条直线的方程，求解二元一次方程组即可得到交点坐标。

在$n$维欧氏空间$\mathbf{R}^n$下，已知两个向量$\boldsymbol{a},\boldsymbol{b}$，它们的夹角为$\theta$，那么：$\boldsymbol{a}\cdot \boldsymbol{b}=|\boldsymbol{a}||\boldsymbol{b}|\cos\theta$

在$n$维欧氏空间$\mathbf{R}^n$下，已知两个向量$\boldsymbol{a}=(a_1,a_2,\dots, a_n),\boldsymbol{b}=(b_1,b_2,\dots,b_n)$，那么：$\boldsymbol{a}\cdot\boldsymbol{b}=\sum_{i = 1}^{n} a_ib_i$

欧拉函数，即$\phi(x)$，代表$x$以内与$x$互质的数的个数。

若$x=p_1^{k_1}p_2^{k_2}...p_n^{k_n}$，则$\phi(x)=x(1-\frac{1}{p_1})(1-\frac{1}{p_1})...(1-\frac{1}{p_n})$。

$\log_aN$中的$a$为对数的底数，$N$为真数。

C++中的log(N)$=\log_eN=\ln N$，其中$log_eN$是自然对数（natural logarihm）

无理数$e=2.718~28$···

“$\log$”是logarithm（对数）的缩写。

弧度指一个角在一个半径为$1$的圆成为圆心角时所对应的弧长，$\cos x$中的$x$的单位是$rad$

如果数列$A$是斐波那契数列，则$a_i=\frac{1}{\sqrt{5}}\big(\big(\frac{1+\sqrt{5}}2\big)^i-\big(\frac{1-\sqrt{5}}2\big)^i\big)$

$\cos^2x+\sin^2x=1$

费马小定理:如果整数$a$,$p$互质或者$\gcd(a,p)=1$，
那么$a^{p-1}\equiv1(\bmod~p)$

$p$为质数,$ax\equiv1(\bmod~p)$,$x=a^{p-2},设a_{1～p-1}为1～p-1\bmod p意义下的逆元,a_1=1,i\not=1,a_i=(p-\lfloor\frac{p}{i}\rfloor)\times a_{p\bmod i}\bmod p$

柯西不等式:$(a_1^2+a_2^2+...+a_n^2)(b_1^2+b_2^2+...+b_n^2)\geqslant(a_1b_1+a_2b_2+...+a_nb_n)^2$

奇函数(odd function):$f(-x)=-f(x)$

偶函数:$f(x)=f(-x)$

杨辉三角的第$i$行第$j$列是$C^{j-1}_{i-1}$，$C^i_j=C_{i-1}^{j-1}+C_{i-1}^j$

由上一段可以知道$C_n^1+C^2_n+...+C_n^n=(C_{n-1}^0+C_{n-1}^1)+(C_{n-1}^1+C_{n-1}^2)+...(C_{n-1}^{n-1}+C_{n-1}^n)=1+2(C_{n-1}^1+C^2_{n-1}+...+C_{n-1}^{n-1})=(\underbrace{111...1}_{n个1})_2=2^n-1$

$\Pi$是连乘，用法与$\sum$相同

字母'A'的ASCII码是41H（0100 0001B），字母'a'的ASCII码是61H（0110 0001B），字母'A'与'a'的二进制后5位是相同的，所以无论是大写字母还是小写字母x，x &31（1 1111B）的值就是x在字母表里的顺序。

c++math.h的函数：

三角函数：

$sin(x)$:$x$的正弦值；值域 $[-1，1]$

$cos(x)$:$x$的余弦值；值域 $[-1，1]$

$tan(x)$:$x$的正切值；值域$（+∞，-∞）$

$asin(x)$计算反正弦；值域 $[-\pi/2，\pi/2]；x∈ [-1，1]$

$atan(x)$计算反正切; 值域 $[-\pi/2，\pi/2]$

$atan2(y,x)$计算具有两个参数的反正切线，值域为$[-\pi,\pi]$

双曲函数：

$sinh$计算双曲正弦

$cosh$计算双曲余弦

$tanh$计算双曲正切

$asinh$计算反双曲正弦

$acosh$计算反双曲余弦

$atanh$计算反双曲正切

指数和对数函数:

$exp(x)$计算底数为$e$的指数函数

$ldexp(x,n)$计算 $x*2^n$的值

$log(x)$计算自然对数$ln(x)$,其中$x>0$

$log10(x)$计算以$10$为底的对数，其中$x>0$

$exp2(x)$计算底数为$2$的指数函数

$expm1（x）$计算$e$的$x$次减一

$log2（x）$计算以$2$为底的对数

其他函数：

$pow(x,y)$计算$x^y$的值

$sqrt(x)$计算$x$的平方根

$cbrt(x)$计算$x$的立方根

$hypot(x,y)$计算$(x^2+y^2)$的平方根，常用于计算三角形的斜边长

$fabs(x)$计算$x$（高精度的$double$，$float$）的绝对值

$abs(x)$计算 $x$（整数）的绝对值