uoj#P976. 【JOISC2025】电路 2
【JOISC2025】电路 2
这是一道交互题。本题中,交互库是非自适应的。
JOI 君正在玩一个电子积木。
该电子积木由 $N$ 个 $\texttt{AND}$ 组件、$N$ 个 $\texttt{OR}$ 组件和一个电路板组成。电路板包含 $2N + 1$ 个开关和 $N$ 个组件插槽,每个组件插槽可以放置一个 $\texttt{AND}$ 组件或 $\texttt{OR}$ 组件。根据放置的组件和开关状态,电路板会输出 $0$ 或 $1$。
电路说明
- 每个开关被分配一个从 $0$ 到 $2N$ 的编号,且每个开关有 $\texttt{ON}$(开启)或 $\texttt{OFF}$(关闭)两种状态。每个开关会按以下规则输出 $0$ 或 $1$。
- 每个组件插槽被分配一个从 $0$ 到 $N - 1$ 的编号。每个组件插槽也会按以下规则输出 $0$ 或 $1$。
每个开关和组件插槽的输出值按从高编号到低编号的顺序确定。若开关和组件插槽编号相同,则先确定组件插槽的输出值。
对于 $j = 2N, 2N - 1, \ldots, N$ 的开关:
- 若开关 $j$ 为 $\texttt{OFF}$,则输出 $0$。
- 若开关 $j$ 为 $\texttt{ON}$,则输出 $1$。
对于 $j = N - 1, N - 2, \ldots, 0$ 的开关:
- 设组件插槽 $j$ 的输出值为 $x$。
- 若开关 $j$ 为 $\texttt{OFF}$,则输出 $x$。
- 若开关 $j$ 为 $\texttt{ON}$,则输出 $1 - x$。
- 对于组件插槽 $i = N - 1, N - 2, \ldots, 0$:
- 它连接到两个开关 $U_i$ 和 $V_i$(满足 $i < U_i < V_i \leq 2N$)。
- 设开关 $U_i$ 的输出为 $x$,开关 $V_i$ 的输出为 $y$。
- 若组件插槽 $i$ 放置的是 $\texttt{AND}$ 组件,则输出 $\min(x, y)$。
- 若组件插槽 $i$ 放置的是 $\texttt{OR}$ 组件,则输出 $\max(x, y)$。
- 对于每个 $j = 1, 2, \ldots, 2N$,存在且仅存在一个 $i$($0 \leq i \leq N - 1$)满足 $U_i = j$ 或 $V_i = j$。
- 电路板的最终输出值等于开关 $0$ 的输出值。
当 $N=3$,且 $U_0=1, V_0=2, U_1=3, V_1=4, U_2=5, V_2=6$ 时,若在组件插槽 $0$ 和 $1$ 放置 $\texttt{AND}$ 组件,在组件插槽 $2$ 放置 $\texttt{OR}$ 组件,其电路结构如下图所示。
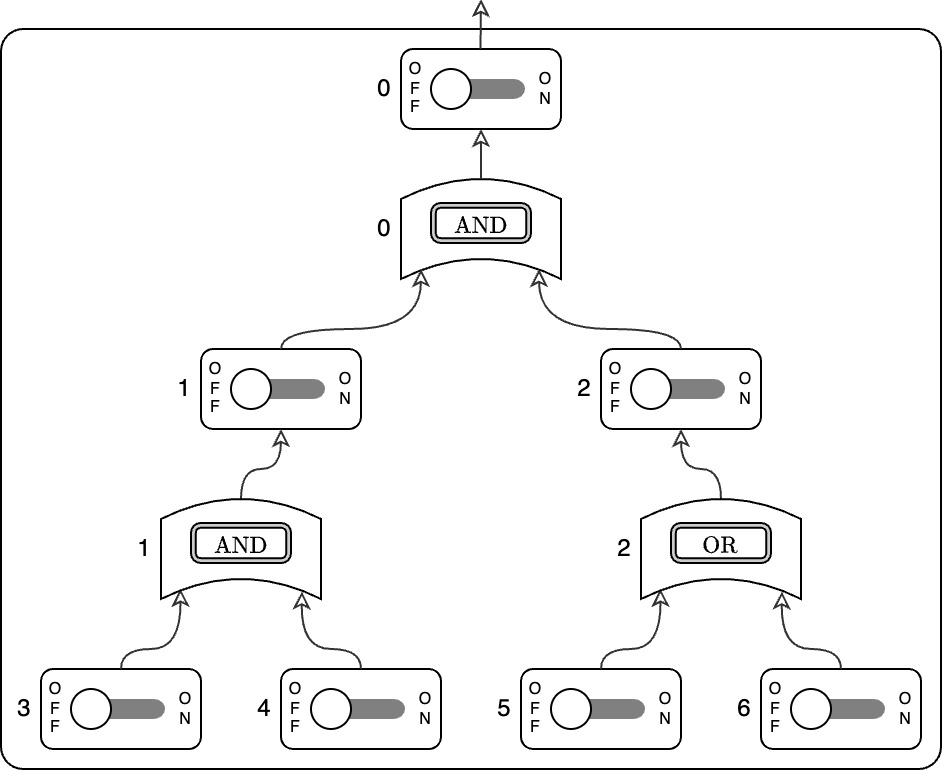
JOI 君原本试图在所有组件插槽中放置 $\texttt{AND}$ 组件,但实际混入了最多 $R$ 个 $\texttt{OR}$ 组件。由于两种组件外观相同,必须通过电路板的输出值来识别。你的任务是通过最多 $1000$ 次查询,确定哪些组件插槽包含 $\texttt{OR}$ 组件。每次查询的格式为:
- 指定所有 $2N + 1$ 个开关的状态。
- JOI 君将根据此配置返回电路板的输出值。
请根据电路板的连接结构和 $\texttt{OR}$ 组件的数量上限,编写一个程序来解决此问题。
实现细节
你不需要,也不应该实现 main 函数。你应当实现以下的函数:
std::string solve(int N, int R, std::vector<int> U, std::vector<int> V)- 此函数在每个测试点中仅被调用一次。
- 参数
N表示组件插槽的数量 $N$。 - 参数
R表示 $\texttt{OR}$ 组件的数量上限 $R$。 - 参数
U和V是长度为 $N$ 的数组,其中U[i]和V[i]($0 \leq i \leq N - 1$)表示组件插槽 $i$ 连接的开关编号 $U_i$ 和 $V_i$。 - 此函数必须返回一个长度为 $N$ 的字符串
t,且满足以下条件:- 对每个 $i = 0, 1, \ldots, N - 1$,若组件插槽 $i$ 包含 $\texttt{AND}$ 组件,则
t[i]必须为 $\texttt{\&}$(&);若包含 $\texttt{OR}$ 组件,则t[i]必须为 $\texttt{|}$(|)。
- 对每个 $i = 0, 1, \ldots, N - 1$,若组件插槽 $i$ 包含 $\texttt{AND}$ 组件,则
- 若返回的字符串
t长度不为 $N$,程序将被判为 $\texttt{Wrong Answer [1]}$。 - 若
t包含 $\texttt{\&}$ 或 $\texttt{|}$ 以外的字符,程序将被判为 $\texttt{Wrong Answer [2]}$。 - 若实际组件类型与
t描述不符,程序将被判为 $\texttt{Wrong Answer [3]}$。
你可以调用以下的函数:
int query(std::string s)- 此函数用于向 JOI 君发起查询。
- 参数
s必须是一个长度为 $2N + 1$ 且仅由'0'和'1'组成的字符串。对每个 $j = 0, 1, \ldots, 2N$:- 若
s[j]为 $\texttt{0}$,则开关 $j$ 设为 $\texttt{OFF}$; - 若
s[j]为 $\texttt{1}$,则开关 $j$ 设为 $\texttt{ON}$。
- 若
- 若
s长度不为 $2N + 1$,程序将被判为 $\texttt{Wrong Answer [4]}$。 - 若
s包含'0'或'1'以外的字符,程序将被判为 $\texttt{Wrong Answer [5]}$。 - 此函数最多调用 $1000$ 次。若超过此限制,程序将被判为 $\texttt{Wrong Answer [6]}$。
- 函数返回值是按
s配置开关后电路板的输出值。
注意事项
- 你可以定义额外的辅助函数或全局变量以供内部使用。
- 你的程序不得使用标准输入/输出或其他文件交互,但可将调试信息输出到标准错误流。
- 实际评测程序是非自适应的(non-adaptive),即交互过程开始时答案已固定。
编译运行
你可以从【附件】中下载包含 Sample Grader 的压缩文件以测试程序。压缩文件中还包含一个示例源代码文件。
Sample Grader 为 grader.cpp。测试时需将 grader.cpp、circuit.cpp 和 circuit.h 置于同一目录。使用以下命令编译:
g++ -std=gnu++20 -O2 -o grader grader.cpp circuit.cpp或执行压缩包中的 compile.sh 脚本。
./compile.sh编译成功后,将生成可执行文件 grader。
注意:实际评测程序与 Sample Grader 不同。 Sample Grader 以单进程运行,从标准输入读取数据并将结果写入标准输出。
输入格式
设 $T$ 为函数 solve 应该返回的长度为 $N$ 的字符串。样例评测程序从标准输入读取以下格式的数据:
$N$ $R$\ $U_{0}$ $V_{0}$\ $U_{1}$ $V_{1}$\ $\vdots$\ $U_{N−1}$ $V_{N−1}$\ $T$
输出格式
样例评测程序将以下信息输出到标准输出:
- 若程序被判定为正确,输出查询调用次数如 $\texttt{Accepted: 22}$;
- 若程序被判定为任何类型的错误答案,输出错误类型如 $\texttt{Wrong Answer [4]}$。
样例评测程序在首次检测到错误条件时立即终止执行。若多个错误条件同时存在,仅显示其中一个。
输入输出样例 #1
输入 #1
1 1 1 2 |
输出 #1
|
样例交互 $1$
| 交互库调用 | 返回值 | 选手程序调用 | 返回值 |
|---|---|---|---|
solve(1, 1, [1], [2]) |
/ | / | / |
| / | / | query("010") |
$1$ |
| / | / | query("011") |
$1$ |
| / | / | query("111") |
$0$ |
| / | "竖线" |
/ | / |
首次调用 query 时的输出计算过程:
- 开关 $1$ 设为 $\texttt{ON}$,开关 $2$ 设为 $\texttt{OFF}$,因此开关 $1$ 输出 $1$,开关 $2$ 输出 $0$。
- 组件插槽 $0$ 包含 $\texttt{OR}$ 组件,连接的开关 $1$ 和 $2$ 分别输出 $1$ 和 $0$,因此组件插槽 $0$ 输出 $\max(1, 0) = 1$。
- 开关 $0$ 设为 $\texttt{OFF}$,而组件插槽 $0$ 输出 $1$,因此开关 $0$ 输出 $1$。
- 最终,电路板的输出为 $1$。
该样例满足所有子任务的限制。
输入输出样例 #2
输入 #2
3 3 1 2 3 4 5 6 &&|
输出 #2
&&|
样例交互 $2$
| 交互库调用 | 返回值 | 选手程序调用 | 返回值 |
|---|---|---|---|
solve(3, 3, [1, 3, 5], [2, 4, 6]) |
/ | / | / |
| / | / | query("0001001") |
$0$ |
| / | / | query("0001110") |
$1$ |
| / | / | query("0000011") |
$0$ |
| / | "&&竖线" | / | / |
题目描述中的电路图对应此示例。
该样例满足子任务 $3,6\sim 9$ 的限制。
附件中:
- $\texttt{sample-01-in.txt}$ 对应样例 1;
- $\texttt{sample-02-in.txt}$ 对应样例 2;
- $\texttt{sample-03-in.txt}$ 满足子任务 $3,4,5,8,9$ 的限制;
- $\texttt{sample-04-in.txt}$ 满足子任务 $3,6\sim 9$ 的限制。
数据范围
- $1 \leq N \leq 8\,000$;
- $1 \leq R \leq \min(N, 120)$;
- 对每个 $i$($0 \leq i \leq N - 1$),满足 $i < U_i < V_i \leq 2N$;
- 对于每个 $j = 1, 2, \ldots, 2N$,存在且仅存在一个 $i$($0 \leq i \leq N - 1$)满足 $U_i = j$ 或 $V_i = j$。
子任务
- $\text{Subtask 1 (1 pts)}$:$N = 1$;
- $\text{Subtask 2 (4 pts)}$:$N \leq 1\,000$ 且 $R = 1$;
- $\text{Subtask 3 (5 pts)}$:$N \leq 1\,000$;
- $\text{Subtask 4 (17 pts)}$:$U_i = i + 1$,$V_i = N + 1 + i$($0 \leq i \leq N - 1$),且 $R \leq 70$;
- $\text{Subtask 5 (8 pts)}$:$U_i = i + 1$,$V_i = N + 1 + i$($0 \leq i \leq N - 1$);
- $\text{Subtask 6 (23 pts)}$:$U_i = 2i + 1$,$V_i = 2i + 2$($0 \leq i \leq N - 1$),且 $R \leq 70$;
- $\text{Subtask 7 (8 pts)}$:$U_i = 2i + 1$,$V_i = 2i + 2$($0 \leq i \leq N - 1$);
- $\text{Subtask 8 (27 pts)}$:$R \leq 70$;
- $\text{Subtask 9 (7 pts)}$:无额外限制。
