Asadullo 是电力与工业优化联盟（Alliance for Power and Industrial Optimization，APIO）的杰出研究员。最近，他研究出利用一种未知材料的发电方法。

这种未知材料不能单独地发电；但如果用这种材料制造出若干极长的杆，这些长杆之间的相互作用能产生电力。

特别地，给定 $n$ 根长杆的属性 $v[0], v[1], \ldots, v[n-1]$。该属性描述了第 $i$ 根长杆放置在与 $x$ 轴正方向逆时针成 $a[i] = 360 \cdot \frac{v[i]}{100000}$ 的角度。这 $n$ 根长杆的发电效率为：

$$\sum_{i < j} \operatorname{acute}(i,j)$$

其中 $\operatorname{acute}(i,j)$ 表示第 $i$ 根长杆和第 $j$ 根长杆所形成的锐角。在本题中，我们认为 $90^\circ$ 也是锐角。形式化地，$\operatorname{acute}(i,j) = \min(|v[i] - v[j]|, 50000 - |v[i] - v[j]|)$。

换句话说，发电效率取决于每对长杆所形成的锐角度数的总和。

例如，当 $v = [5000, 12500, 37500]$ 则相应地 $a = [18, 45, 135]$，我们将得到下图：

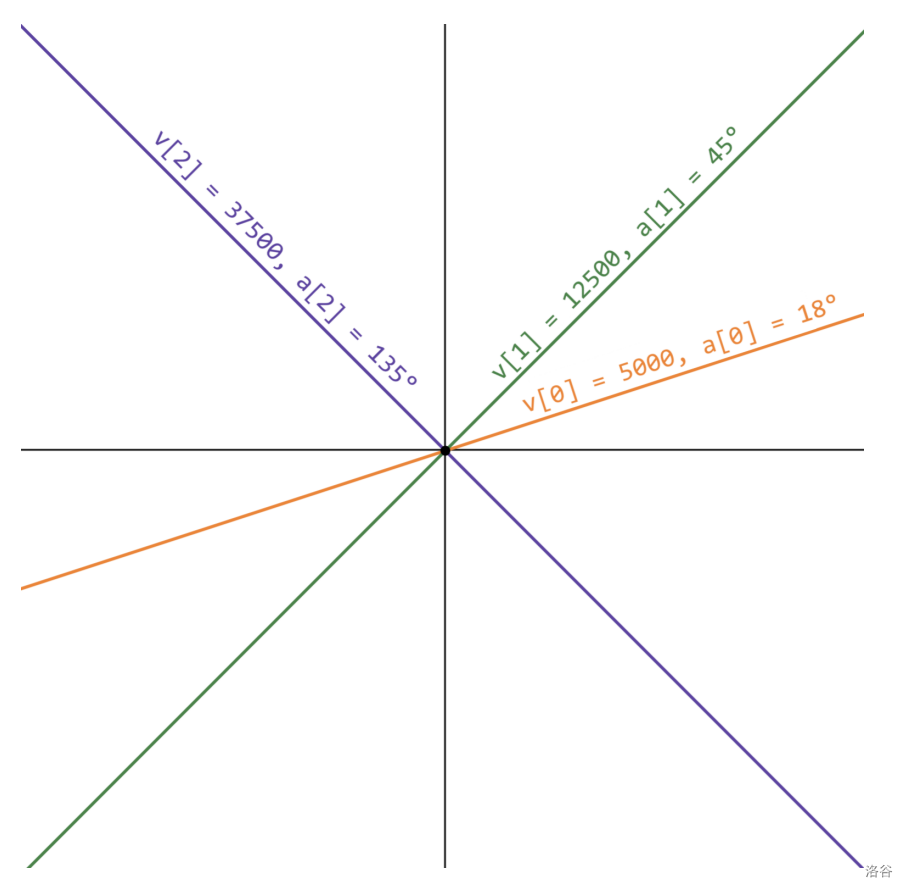
此图中，$\operatorname{acute}(0,1) = 7500$（即 $27^\circ$），$\operatorname{acute}(0,2) = 17500$（即 $63^\circ$），以及 $\operatorname{acute}(1,2) = 25000$（即 $90^\circ$）。因此，这些长杆的发电效率等于 $7500 + 17500 + 25000 = 50000$。

Asadullo 想要调整这 $n$ 根长杆的相对角度以最大化发电效率。然而，存在以下约束条件：

• 首先，由于长杆的材料对生命体具有极高危害，这些长杆只能在受控的方式下操作一个特殊的机械装置来转动。这个装置允许选择若干长杆，并将所有选择的长杆转动相同的角度。
• Asadullo 不希望这些长杆的发电效率降低。因此，每次操作后，发电效率都不能低于转动前的发电效率。
• 由于操作这个装置需要耗费大量的能量，所有操作里被选择的长杆总数不能超过 2000000。

在这些约束条件下，Asadullo 希望执行最优的若干操作，来最大化这些长杆的发电效率。写一段代码来帮助 Asadullo 实现最大可能的发电效率。

实现细节

你需要实现以下函数：

void energy(int n, std::vector<int> v)

• n：长杆的数目。
• v：大小为 n 的数组描述这些长杆的属性。
• 这个函数给调用一次。

在上述函数里，你可以调用以下函数：

void rotate(std::vector<int> t, int x)

• t：互不相同的元素组成的下标数组，即对任意 i 有 $0 \leq t[i] < n$，且对任意 $i < j$ 有 $t[i] \neq t[j]$。数组 t 不要求有序。
• 这个函数将下标数组 t 所选择的长杆同时转动 x 个单位。那么，每个在 t 数组的元素 i，将使 v[i] 变成 $(v[i] + x) \mod 50000$。
• 这个函数可以被调用多次。数组 t 在所有调用里的累加长度不能超过 2000000。

例子

例 1

考虑以下函数调用：

energy(2, [20000, 10000])

此处，$v = [20000, 10000]$ 且初始的发电效率为 $20000 - 10000 = 10000$。以下是一种可能的场景：

1. 调用 rotate([0, 1], 8000)。那么 v 变成 [28000,18000]。发电效率保持不变。
2. 调用 rotate([0], 15000)。那么 v 变成 [43000,18000]。发电效率变成 $43000 - 18000 = 25000$。

可以证明，对于初始配置，25000 是能实现的最大发电效率。因此，Asadullo 可以停止操作。

例 2

考虑以下函数调用：

energy(3, [5000, 12500, 37500])

题面的示例插图描述的就是这个例子，可以证明，初始配置实现的即是最大的发电效率。所以，不需要执行任何操作。

约束条件

• $2 \leq n \leq 100 \, 000$
• 对任意的 $0 \leq i < n$，满足 $0 \leq v[i] \leq 49 \, 999$
• 数组 v 的元素不一定互不相同

子任务

1. (5 分) $n = 2$
2. (11 分) 对于每个 $0 \leq i < n$，均有 $v[i] < 25 \, 000$
3. (8 分) $n \leq 10$
4. (15 分) $n \leq 100$
5. (15 分) $n \leq 300$
6. (20 分) $n \leq 2000$
7. (26 分) 没有额外的约束条件。

评测程序示例

评测程序示例按以下格式读取输入：

• 第 1 行：$n$
• 第 2 行：$v[0] \, v[1] \ldots \, v[n-1]$

评测程序示例按以下格式打印输出：

• 第 1 行：长杆最终的发电效率

此外，评测程序示例会将你所调用的转动操作的详细信息写入 log.txt 文件。