uoj#P965. 【APIO2025】排列游戏
【APIO2025】排列游戏
Alice 和 Bob 是童年时代的朋友,他们喜欢玩智力游戏。今天,他们在玩一个关于图的新游戏。
游戏中包含一个连通图,具有 $m$ 个顶点,编号为 $0$ 到 $m-1$,以及 $e$ 条边,编号为 $0$ 到 $e-1$。第 $i$ 条边连接顶点 $u[i]$ 和 $v[i]$。
游戏中还包含一个长度为 $n$ 的排列 $p[0], p[1], \ldots, p[n-1]$,其中 $m \leq n$。排列是一个数组,其中从 $0$ 到 $n-1$ 的每个数字以某种顺序仅出现一次。排列 $p$ 的分数是满足 $p[i] = i$ 的下标 $i$ 的数量。
游戏最多持续 $10^{100}$ 个回合。在每个回合中,都会发生以下情况:
- 如果 Alice 决定结束游戏,游戏终止。
- 否则,Alice 选择一组两两不同的下标 $t[0], t[1], \ldots, t[m-1]$,满足 $0 \leq t[i] < n$。请注意,游戏不要求 $t[0] < t[1] < \ldots < t[m-1]$。
- Bob 选择一个图中边的下标 $0 \leq j < e$,并交换 $p[t[u[j]]]$ 和 $p[t[v[j]]]$。
Alice 希望能最大化排列的最终分数而 Bob 希望最小化排列的最终分数。
你的任务是帮助 Alice,与由评测程序模拟的 Bob 进行游戏。
定义一局游戏的“最优分数”为当 Alice 和 Bob 都采用最优策略进行游戏时最终得到的排列的分数。
你需要求出本局游戏的最优分数,然后与 Bob 进行游戏,且需要在若干轮后至少达到最优分数。
请注意:你实现的 Alice 的策略应当是普适性的,能够处理 Bob 可能采用的各种策略,即使 Bob 采用的策略可能并非最优。
实现细节
你要实现以下函数:
int Alice(int m, int e, std::vector<int> u, std::vector<int> v, int n, std::vector<int> p)m: 图中顶点个数。e: 图中边的数量。u和v: 长度为e的数组,描述图中的边。n: 排列的长度。p: 长度为n的数组,描述排列。
该函数恰好被调用一次。 该函数应该返回一个整数,即游戏的最后分数,假设 Alice 和 Bob 都以最优策略玩游戏。
在该函数中,你可以调用以下函数:
int Bob(std::vector<int> t)t: 长度为 $m$ 的数组,包含一组两两不同的下标,满足 $0 \leq t[i] < n$ 且对于任意 $i \neq j$ 均有 $t[i] \neq t[j]$。- 该函数返回一个整数 $j$,满足 $0 \leq j < e$。
- 该函数可以被调用多次。
例子
考虑以下调用:
Alice(5, 6, [4, 0, 3, 1, 4, 2], [2, 2, 0, 2, 0, 3], 10, [8, 2, 7, 6, 1, 5, 0, 9, 3, 4])如下图所示:
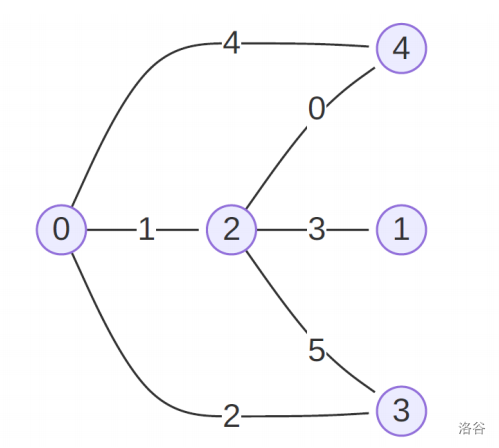
$p$ 的初值为 $[8, 2, 7, 6, 1, 5, 0, 9, 3, 4]$。
给定以上约束条件,我们可以证明排列的最优分数为 1。
假设,Alice 做了以下 4 次操作:
| 给 Bob 的参数 $t$ | Bob 返回的值 | $p$ 对应的下标 | Bob 交换后的 $p$ |
|---|---|---|---|
| [3, 1, 5, 2, 0] | 5 | 5, 2 | [8, 2, 5, 6, 1, 7, 0, 9, 3, 4] |
| [9, 3, 7, 2, 1] | 0 | 1, 7 | [8, 9, 5, 6, 1, 7, 0, 2, 3, 4] |
| [5, 6, 7, 8, 9] | 1 | 5, 7 | [8, 9, 5, 6, 1, 2, 0, 7, 3, 4] |
| [7, 5, 2, 3, 6] | 3 | 5, 2 | [8, 9, 2, 6, 1, 5, 0, 7, 3, 4] |
注意 Alice 和 Bob 所做的操作不一定是最优的。上面显示的操作纯粹是为了演示。另外,注意到 Alice 实际上可以在一开始就结束游戏,因为最开始的排列分数已经达到了最优分数 1。
在 Alice 做了上述所有操作后,排列的实际分数为 $3$($p[2] = 2$, $p[5] = 5$, $p[7] = 7$)。
函数 Alice() 最后返回值为 1,即排列的最优分数。
请注意,即使 Alice 通过与 Bob 玩游戏获得了分数 3,但如果函数 Alice() 的返回值是 3 而不是 1,你将获得 0 分。
约束条件
- $2 \leq m \leq 400$
- $m - 1 \leq e \leq 400$
- $0 \leq u[i], v[i] < m$
- $m \leq n \leq 400$
- $0 \leq p[i] < n$
图是连通的,并且没有自环和重边。 $p$ 是一个排列,即对任意 $i \neq j$, $p[i] \neq p[j]$。
子任务
- (6 分) $m = 2$
- (6 分) $e > m$
- (10 分) $e = m - 1$
- (24 分) $e = m = 3$
- (24 分) $e = m = 4$
- (30 分) $e = m$
对于每个子任务,你可以获得部分分数。设 $r$ 是 $\frac{k}{n}$ 在某个子任务的所有测试用例中的最大比值,其中 $k$ 是回合数(即对 Bob() 的调用次数)。那么,你在该子任务的得分为该子任务的满分乘以以下数字:
| 条件 | 乘数 |
|---|---|
| $12 \leq r$ | 0 |
| $3 < r < 12$ | $1 - \log_{10}(r - 2)$ |
| $r \leq 3$ | 1 |
特别地,如果在 $3n$ 个回合内解决问题,则该子任务将获得满分。使用超过 $12n$ 个回合将导致该子任务获得 0 分(显示为 output isn't correct)。
评测程序示例
评测程序示例按以下格式读取输入:
- 第 1 行: $m$
- 第 $2 + i$ 行 $(0 \leq i \leq e - 1)$: $u[i]\, v[i]$
- 第 $2 + e$ 行: $n$
- 第 $3 + e$ 行: $p[0]\, p[1]\, \ldots\, p[n - 1]$
评测程序示例按以下格式打印你的答案:
- 第 1 行: 最后排列 $p$
- 第 2 行:
Alice()的返回值 - 第 3 行: 最后排列的实际得分
- 第 4 行: 回合数
