在JOI动物园里有 $2N$ 只变色龙，从 $1$ 到 $2N$ 编号。在它们中有 $N$ 只变色龙的性别是 X，另外 $N$ 只的性别是Y。

每个变色龙都有自己的原色。变色龙的原色具有以下性质：

• 同性变色龙的原色是两两不同的。
• 每只变色龙都有一只原色相同的异性变色龙。

现在，JOI动物园到了爱情的季节。每只变色龙都爱另一只变色龙。变色龙的爱具有以下性质：

• 每只变色龙恰好爱一只异性变色龙。
• 每只变色龙爱的变色龙和它自己原色不同。
• 所有变色龙爱的变色龙两两不同。

你可以聚集一些变色龙组织一场见面会。对每只参加见面会的变色龙$s$，记它爱的变色龙为$t$，$s$的颜色由以下规则决定：

• 如果$t$也参加了见面会，$s$的颜色是$t$的原色。
• 否则， $s$的颜色是$s$的原色。

变色龙的颜色在不同的见面会中可能不保持一致。对于每场见面会，你可以数出参加的变色龙有多少不同的颜色。

你想通过举行至多$20000$场见面会来确定每对有着相同原色的变色龙。

实现细节

你的程序需要包含chameleon.h。

• 要实现函数void Solve(int N)

这个函数在每个测试点中会被调用恰好一次。$N$表示具有每种性别的变色龙的数量。（也就是说，一共有$2N$只变色龙。）

你的程序可以调用以下函数：

1. `int Query(const std::vector &p)

你可以通过调用这个函数来举行一场见面会。

• $p$是来参加见面会的变色龙的编号列表。
• 返回值是来参加见面会的变色龙的颜色种数。
• 每个$p$中的元素都应不小于$1$，不大于$2N$。否则你的程序将被判为Wrong Answer [1]。
• $p$中的元素应两两不同。否则你的程序将被判为Wrong Answer [2]。

• 你的程序不能调用这个函数超过$20000$次。否则你的程序将被判为Wrong Answer [3]。

• void Answer(int a, int b)

你可以通过这个函数来报告一对具有相同原色的变色龙。

• 参数$a,b$表示变色龙$a,b$具有相同的原色。
• 必须保证$1 \leq a,b \leq 2N$。否则你的程序将被判为Wrong Answer [4]。
• 不能对同一对$a,b$调用超过一次这个函数。否则你的程序将被判为Wrong Answer [5]。
• 如果变色龙$a$和$b$的原色不同，你的程序将被判为Wrong Answer [6]。
• 你的程序应该恰好调用这个函数$N$次。否则你的程序将被判为Wrong Answer [7]。

重要提示

• 你的程序可以定义全局变量或其他函数。
• 你的程序不需要也不应该访问标准输入输出，也不应该访问任何文件。

本机测试的方法

将grader.cpp和chameleon.cpp，chameleon.h放在当前目录下，运行

g++ -std=gnu++14 -O2 -o grader grader.cpp chameleon.cpp

当编译成功时，文件grader将被生成。

样例交互库的输入格式

样例交互库从标准输入读取以下数据：

$N$

$Y_1 \cdots Y_{2N}$

$C_1 \cdots C_{2N}$

$L_1 \cdots L_{2N}$

$Y_i$表示第$i$只变色龙的性别，取值范围是${0,1}$，分别表示性别X和Y。

$C_i$表示第$i$只变色龙的原色，取值范围是$[1,N]$中的整数。

$L_i$表示第$i$只变色龙爱的变色龙的编号。

样例交互库的输出格式

当你的程序顺利结束时，样例交互库将向标准输出写入以下内容：

• 如果你的程序运行结果正确，将输出你的程序调用Query的次数。比如Acepted: 100
• 如果你的程序答案错误，将输出错误类型。比如Wrong Answer [1]

如果你的程序同时触发了多种类型的错误，交互库只会报告其中的一种。

限制与约定

• $2 \leq N \leq 500$
• $0 \leq Y_i \leq 1 (1 \leq i \leq 2N)$
• $1 \leq C_i \leq N (1 \leq i \leq 2N)$
• 对任意$j(1 \leq j \leq N)$，有且仅有一个$i(1 \leq i \leq 2N)$使$Y_i=0,C_i=j$
• 对任意$j(1 \leq j \leq N)$，有且仅有一个$i(1 \leq i \leq 2N)$使$Y_i=1,C_i=j$
• $1 \leq L_i \leq 2N(1 \leq i \leq 2N)$
• $Y_i \neq Y_{L_i} (1 \leq i \leq 2N)$
• $C_i \neq C_{L_i} (1 \leq i \leq 2N)$
• $L_k \neq L_l (1 \leq k < l \leq 2N)$

子任务

1. (4 分) $L_{L_i} = i(1 \leq i \leq 2N)$
2. (20 分) $N \leq 7$
3. (20 分) $N \leq 50$
4. (20 分) $Y_i=0(1 \leq i \leq N)$
5. (36 分) 没有特殊限制

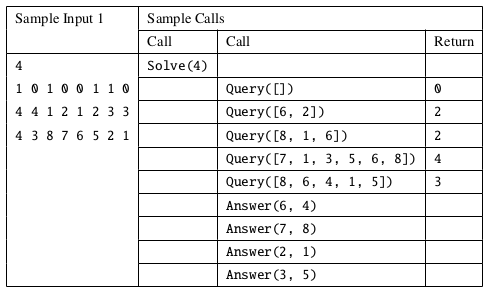
样例交互过程

下载

样例及测评库下载