uoj#P1000. 【IOI2025】世界地图
【IOI2025】世界地图
玻利维亚考古学家 Pacha 先生在 Tiwanaku 附近发现了一份古代文献,描述了 Tiwanaku 时期(公元 300–1000 年)的世界。当时有 $N$ 个国家,从 $1$ 到 $N$ 编号。
文献中列出了 $M$ 对不同的相邻国家:
$$(A[0], B[0]), (A[1], B[1]), \ldots, (A[M-1], B[M-1]).$$
对每个 $i$($0 \leq i < M$),文献指出国家 $A[i]$ 与国家 $B[i]$ 相邻,反之亦然。文献中未列出相邻关系的国家之间是不相邻的。
Pacha 先生希望绘制一幅世界地图,使得各国之间的相邻关系恰好与 Tiwanaku 时期完全一致。为此,他首先选择一个正整数 $K$。然后,他将地图绘制为一个由 $K \times K$ 的方格组成的网格,方格的行从 $0$ 到 $K-1$ 编号(从上到下),列从 $0$ 到 $K-1$ 编号(从左到右)。
Pacha 先生希望用 $N$ 种颜色来为地图的每个方格着色。颜色从 $1$ 到 $N$ 编号,颜色 $j$($1 \leq j \leq N$)代表国家 $j$。着色方案必须满足以下所有条件: 对每个 $j$($1 \leq j \leq N$),至少有一个方格染成了颜色 $j$。 对每对相邻国家 $(A[i], B[i])$,至少存在一对相邻的方格,其中一个方格染成了颜色 $A[i]$,另一个染成了颜色 $B[i]$。如果两个方格有一条公共边,则认为它们是相邻的。 * 对于任意一对相邻且颜色不同的方格,它们所代表的国家在 Tiwanaku 时期也必须是相邻的。
例如,若 $N = 3$,$M = 2$,且相邻国家为 $(1,2)$ 和 $(2,3)$,则国家 $1$ 与 $3$ 不相邻。下图是一幅 $K = 3$ 的地图,满足所有条件。
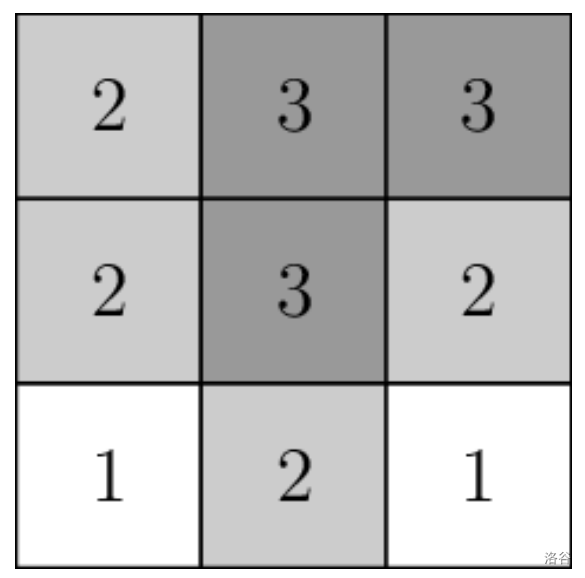
特别地,一个国家不必在地图上形成连通区域。在上述地图中,国家 3 是连通区域,而国家 1 和国家 2 则不是连通区域。
你的任务是帮助 Pacha 先生选择一个 $K$ 的值,并据此绘制一幅地图。文献保证这样的地图一定存在。由于 Pacha 先生倾向于更小的地图,因此在最后一个子任务中,你的得分取决于 $K$ 的大小。$K$ 越小,可能的得分越高。不过,本题无需找出可能的最小 $K$ 值。
实现细节
你要实现以下函数:
std::vector<std::vector<int>> create_map(int N, int M,
std::vector<int> A, std::vector<int> B)- $N$:国家的数量。
- $M$:国家之间的相邻关系的数量。
- $A$ 和 $B$:长度为 $M$ 的数组,描述国家之间的相邻关系。
- 对每个测试用例,该函数最多被调用 50 次。
该函数应返回一个数组 $C$,表示地图。 设 $C$ 的长度为 $K$。 $C$ 的每个元素都必须是一个长度为 $K$ 的数组,数组的元素为 $1$ 到 $N$ 之间的整数。 $C[i][j]$ 表示第 $i$ 行、第 $j$ 列的方格的颜色(对所有满足 $0 \leq i, j < K$ 的 $i$ 和 $j$)。 * $K$ 必须小于或等于 $240$。
输入格式
输入的第一行包含一个整数 $T$,表示场景的数量。 接下来是 $T$ 个场景的描述,每个场景的格式如下。
输入格式:
N M A[0] B[0] : A[M-1] B[M-1]
输出格式
输出格式:
P Q[0] Q[1] ... Q[P-1]C[0][0] ... C[0][Q[0]-1] : C[P-1][0] ... C[P-1][Q[P-1]-1]
其中, 是 create_map 返回的数组 的长度,(0 \leq i < P)是 的长度。注意,输出格式中的第 3 行是有意留空的。
输入输出样例 #1
输入 #1
3 2 1 2 2 3
输出 #1
3 3 3 3 2 3 3 2 3 2 1 2 1
输入输出样例 #2
输入 #2
4 4 1 2 1 3 2 4 3 4
输出 #2
7 7 7 7 7 7 7 7 2 1 3 3 4 3 4 2 1 3 3 3 3 3 2 1 1 1 3 4 4 2 2 2 1 3 4 3 1 1 1 2 4 4 4 2 2 1 2 2 4 3 2 2 1 2 2 4 4
说明/提示
例子
在 CMS 中,以下两个场景包含在同一个测试用例中。
例 1
考虑以下调用:
create_map(3, 2, [1, 2], [2, 3])
这是题目描述中的例子,该函数可以返回如下地图。
[ [2, 3, 3], [2, 3, 2], [1, 2, 1] ]
例 2
考虑以下调用:
create_map(4, 4, [1, 1, 2, 3], [2, 3, 4, 4])
在这个例子中,$N = 4$,$M = 4$,国家 $(1, 2)$、$(1, 3)$、$(2, 4)$ 和 $(3, 4)$ 之间是相邻的。 因此,国家 $(1, 4)$ 和 $(2, 3)$ 之间并不相邻。
该函数可以返回如下 $K = 7$ 的地图,该地图满足所有条件。
[ [2, 1, 3, 3, 4, 3, 4], [2, 1, 3, 3, 3, 3, 3], [2, 1, 1, 1, 3, 4, 4], [2, 2, 2, 1, 3, 4, 3], [1, 1, 1, 2, 4, 4, 4], [2, 2, 1, 2, 2, 4, 3], [2, 2, 1, 2, 2, 4, 4] ]
不过地图可以更小;例如,该函数也可以返回如下 $K = 2$ 的地图。
[ [3, 1], [4, 2] ]
注意,两幅地图都满足 $K/N \leq 2$。
约束条件
- $1 \le N \le 40$
- $0 \le M \le \frac{N \cdot (N - 1)}{2}$
- 对每个满足 $0 \le i < M$ 的 $i$,有 $1 \le A[i] < B[i] \le N$。
- 二元组 $(A[0], B[0]), \ldots, (A[M - 1], B[M - 1])$ 互不相同。
- 至少存在一幅地图,能够满足所有条件。
子任务与评分规则
| 子任务 | 分数 | 额外的约束条件 |
|---|---|---|
| 1 | $5$ | $M = N - 1$,对每个 $0 \le i < M$,有 $A[i] = i + 1$,$B[i] = i + 2$。 |
| 2 | $10$ | $M = N - 1$ |
| 3 | $7$ | $M = \frac{N \cdot (N - 1)}{2}$ |
| 4 | $8$ | 国家 $1$ 与所有其他国家相邻。其他国家之间也可能相邻。 |
| 5 | $14$ | $N \leq 15$ |
| 6 | $56$ | 没有额外的约束条件。 |
在子任务 6 中,你的得分取决于 $K$ 的值。
如果 create_map 返回的任一地图不满足所有条件,则该子任务的得分为 $0$。
否则,令 $R$ 为所有对 create_map 的调用中 $K / N$ 的最大值。根据下表,你将获得部分得分:
| 范围 | 分数 |
|---|---|
| $6 < R$ | $0$ |
| $4 < R \leq 6$ | $14$ |
| $3 < R \leq 4$ | $28$ |
| $2.5 < R \leq 3$ | $42$ |
| $2 < R \leq 2.5$ | $49$ |
| $R \leq 2$ | $56$ |
