题目描述
19 世纪初,统治者下令在俯瞰美丽河景的高原上建造一座宫殿。这块高原被看做是一个由正方形单元格组成的 n×m 网格。网格的行从 0 到 n−1 编号,列从 0 到 m−1 编号。第 i 行第 j 列(0≤i≤n−1,0≤j≤m−1)的单元格记为单元格 (i,j)。每个单元格 (i,j) 有特定的海拔高度,记为 ai,j。
统治者指示他的建筑师选择一个矩形区域来建造宫殿。该区域不能包含网格边界(第 0 行,第 n−1 行,第 0 列,以及第 m−1 列)上的任何单元格。为此,建筑师应选出四个整数 r1,r2,c1 和 c2(1≤r1≤r2≤n−2 且 1≤c1≤c2≤m−2),对应于包括所有满足 r1≤i≤r2 且 c1≤j≤c2 的单元格 (i,j) 的矩形区域。
此外,一个区域被认为是合法的,当且仅当对于该区域中的每个单元格 (i,j),以下条件成立:对于与该区域相邻的、位于第 i 行的两个单元格(单元格 (i,c1−1) 和 (i,c2+1)),以及与该区域相邻的、位于第 j 列的两个单元格(单元格 (r1−1,j) 和 (r2+1,j)),单元格 (i,j) 的海拔高度必须严格小于这四个单元格的海拔高度。
你的任务是帮助建筑师统计可建宫殿的合法区域的数量(也就是所对应区域为合法的 r1,r2,c1 和 c2 的数量)。
输入格式
第一行,两个整数 n 和 m,表示网格的长和宽。
接下来 n 行,第 i 行 m 个整数,为 ai−1,0…m−1。
输出格式
一行,一个整数,表示合法区域的数量。
6 5
4 8 7 5 6
7 4 10 3 5
9 7 20 14 2
9 14 7 3 6
5 7 5 2 7
4 5 13 5 6
6
提示
样例解释
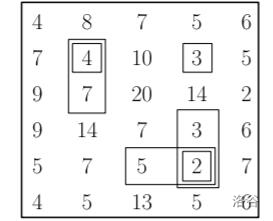
一共有 6 个合法区域,分别为:
- r1=r2=1,c1=c2=1
- r1=1,r2=2,c1=c2=1
- r1=r2=1,c1=c2=3
- r1=r2=4,c1=2,c2=3
- r1=r2=4,c1=c2=3
- r1=3,r2=4,c1=c2=3
例如,r1=1,r2=2,c1=c2=1 对应一个合法区域,原因是以下两个条件都成立:
- a1,1=4 严格小于 a0,1=8,a3,1=14,a1,0=7,和 a1,2=10。
- a2,1=7 严格小于 a0,1=8,a3,1=14,a2,0=9,和 a2,2=20。
数据范围
对于所有数据:
- 1≤n,m≤2500。
- $0 \le a_{i,j} \le 7 \times 10^6 (0 \le i \le n - 1, 0 \le j \le m - 1)$。
详细子任务附加限制与分值如下表:
| 子任务编号 |
附加限制 |
分值 |
| 1 |
n,m≤30 |
8 |
| 2 |
n,m≤80 |
7 |
| 3 |
n,m≤200 |
12 |
| 4 |
n,m≤700 |
22 |
| 5 |
n≤3 |
10 |
| 6 |
0≤ai,j≤1 |
13 |
| 7 |
没有任何附加限制 |
28 |

