luogu#P5009. [yLOI2018] 不老梦
[yLOI2018] 不老梦
题目背景
于万人中万幸得以相逢,刹那间澈净明通。
成为我所向披靡的勇气和惶恐,裂山海,堕苍穹。
——银临《不老梦》。
本题原名《毒瘤分块题》。
题目描述
扶苏非常喜欢一边听古风歌一边写毒瘤分块题。所以这个题的题面恶意卡了分块。
给你一个序列,这个序列中的每个数字有三个参数 。这个序列中的数有一个非常神奇的有关时间的性质:每过一个时刻,序列中第 个数字的值 会增加 。
现在扶苏会对你做出一些询问和对序列进行一些修改。每次操作形如:
- 查询第 时刻区间 的 之和是多少。
- 在第 时刻修改区间 内的 ,将之整体加上一个整数 。
- 在第 时刻修改区间 内的 ,将之整体加上一个整数 。
- 在第 时刻修改区间 内的 ,将之整体加上一个整数 。
规定初始时刻为时刻 。
输入格式
每个测试点有且仅有一组测试数据。
输入的第一行是两个用空格隔开的整数,分别代表序列的长度 以及操作的个数 。
下面 行,每行 个用空格隔开的整数,第 行的整数 分别代表第 个位置的三个参数。
下面 行,每行第一个数是 ,代表操作的种类。
- 对于 的情况,代表对序列进行一次查询。 后有三个用空格隔开的整数 ,代表查询时刻 区间 中 的和。
- 对于 的情况,代表对序列的 值进行一次修改。 后有四个用空格隔开的整数 ,代表在第 时刻将区间 中 的值加上 。
- 对于 的情况,代表对序列的 值进行一次修改。 后有四个用空格隔开的整数 ,代表在第 时刻将区间 中 的值加上 。
- 对于 的情况,代表对序列的 值进行一次修改。 后有四个用空格隔开的整数 ,代表在第 时刻将区间 中 的值加上 。
数据保证参数 是单调递增的,不存在同一时刻有超过一种查询或询问。
输出格式
对于每次查询操作,输出一个一行一个整数,代表查询的答案对 取模的答案。
5 5
1 2 3
4 5 6
7 8 9
10 11 12
13 14 15
2 1 1 3 2
1 3 2 3
3 4 1 4 -3
4 5 1 3 -5
1 6 1 5
377
2708
提示
【样例输入输出 1 解释】
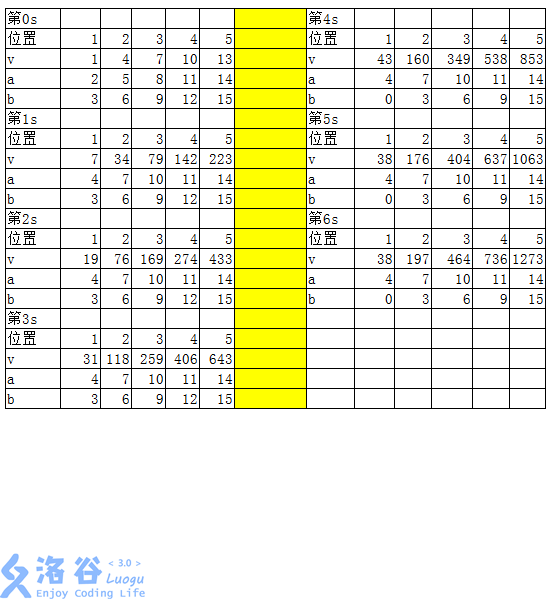
【数据规模与约定】
本题共有 个测试点,各测试点不等分。每个测试点的 的规模如下表。
| 测试点编号 | 测试点编号 | ||
|---|---|---|---|
各测试点分值:
- 对于第 到第 个测试点,每个测试点 分。
- 对于第 到第 个测试点,每个测试点 分。
各测试点 的取值:
- 对于测试点 ,。
- 对于测试点 ,。
- 对于第 到第 个测试点,。
各测试点特殊性质:
- 对于所有 末位数字为 的测试点,满足性质:操作所用到的时刻从 开始,每次增加 。
- 对于所有 末位数字为 的测试点,满足性质:所有修改操作只涉及对 的修改,且修改区间 。
- 对于所有 末位数字为 的测试点,满足性质:所有修改操作只涉及对 的修改。
- 对于所有 末位数字为 的测试点,满足性质:所有修改操作不涉及对 的修改,且对于 的修改满足 。
- 对于所有 末位数字为 的测试点,满足性质:不存在修改操作。
对于全部的测试点,保证 ,,给出的所有数字都在 32 位带符号整形的范围内, 为正数,且按照严格的升序给出。
【提示】
- 请注意数据读入对程序效率造成的影响。
- 请注意常数因子对程序效率造成的影响。
- 的末位数字可以帮助你快速判断测试点的特殊性质。
- 当你的答案为负时,请将其取模成非负数后再进行输出。
