luogu#P11081. [ROI 2019] 自动驾驶 (Day 1)
[ROI 2019] 自动驾驶 (Day 1)
题目背景
翻译自 ROI 2019 D1T2。
今天,需要在因诺波利斯的主广场上,展示最新试验的自动驾驶出租车的功能。广场是一个长 米、宽 米的矩形区域,被划分成 个单位方块。矩形的行从 到 编号,列从 到 编号。因此,每个方块可以由两个正整数 和 表示,分别代表所在行和列的编号。自动驾驶出租车可以在相邻的方块之间移动,每一步可以从当前方块移动到与之相邻的四个方块之一。
今年冬天下了很多雪,所以在展示自动驾驶出租车功能的过程中会用自动除雪机清理广场上的雪。由于自动驾驶交通系统正在测试阶段,因此广场上同一时间只能同时存在一辆自动驾驶交通工具(自动除雪机或自动驾驶出租车)。
由于整个展示期间一直在下雪,自动驾驶出租车的工程师决定借机发挥,展示出租车克服雪堆的能力。
题目描述
每个时刻广场上每个单位方块的雪深可以由一个非负整数表示,自动驾驶出租车的最大可通过雪深也由一个非负整数表示。在移动时,出租车只能停留在雪深不超过最大可通过雪深的方块上。每次展示自动驾驶出租车时,工程师可以设置出租车的最大可通过雪深。
初始状态下,广场上所有方块的雪深为零。每个小时开始时,每个方块的雪深增加一。随后,自动驾驶交通系统可以执行以下三个操作之一,每个操作需要一小时:
- 沿着某一行启动除雪机,然后该行的所有方块的雪深变为零;
- 沿着某一列启动除雪机,然后该列的所有方块的雪深变为零;
- 展示自动驾驶出租车的功能:设置出租车的最大可通过雪深,选择起始和目标方格,并让出租车从起始方块到达目标方块。
只有当存在一个以起始方块开始、以目标方块结束的单位方块序列,其中任意相邻的两个方块有共同的边界,并且序列中每个方块的雪深都不超过出租车的最大可通过雪深时,才可以从起始方块到达目标方块。如果设置的最大可通过雪深允许完成旅行,则出租车应选择步数最少的路径。
每次展示自动驾驶出租车时,需要确定是否可以顺利完成这次的展示(是否有从起始方块到目标方块的路径),如果可以,则需要知道完成此次旅行所需的最少步数。
输入格式
第一行包含三个整数 ,分别表示区域的大小和无人驾驶出租车的操作数。
接下来的 行,每行输入一种操作,其中第 行有以下三种操作类型之一:
1 ri:在第 行启动除雪机。2 ci:在第 列启动除雪机。3 ri1 ci1 ri2 ci2 ki:设置出租车的最大可通过雪深为 ,并尝试从起始方格 开始行驶到结束方格 。
保证输入数据中至少存在一个类型为 的操作。
输出格式
对于每个类型为 的操作,需要输出一行一个整数。如果从起始方格到结束方格的行程是可行的,则输出需要实现该行程的最小步数。如果行程不可行,则输出 -1。
4 3 9
3 2 1 3 3 1
3 2 1 3 3 1
2 1
2 3
1 1
3 2 1 3 3 3
3 2 1 3 3 3
2 2
3 2 1 3 3 6
3
-1
5
-1
3
提示
样例解释:
图中显示了每次操作前广场上的雪层深度以及每次成功尝试从一个方块到另一个方块的出租车最佳路线。
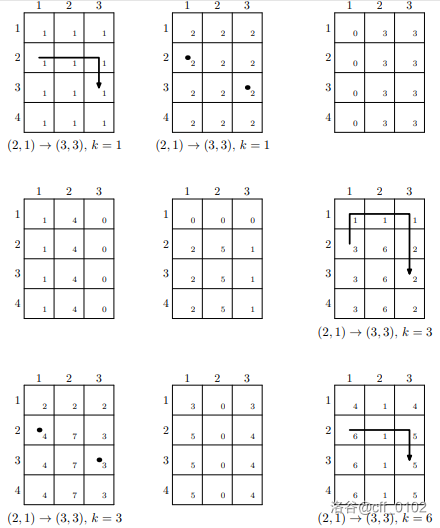
数据范围:
| 子任务 | 特殊性质 | ||
|---|---|---|---|
| 输入中没有操作 | |||
| 操作 中的 均相同 | |||
