luogu#P10857. 【MX-X2-T6】「Cfz Round 4」Ad-hoc Master
【MX-X2-T6】「Cfz Round 4」Ad-hoc Master
题目背景
原题链接:https://oier.team/problems/X2F。
意気込むことはないけれど
尽管不会每天干劲十足
生きていけるよ 君をさがして
但我会继续一边寻找着你一边生活
题目描述
给定一个正整数 。我们令 。
现给出对于每个不大于 的正整数 和不大于 的正整数 所对应的 的值,你需要构造一组数对 ,满足 ,,且存在一棵层数为 的满二叉树 满足:
- 满二叉树 中所有结点的编号形成 的一个排列,且每个结点都有权值;
- 满二叉树 的根结点为结点 ;
- 满二叉树 中每个结点的权值都为小于 的非负整数,且根结点的权值为 ;
- 对于每个不大于 的正整数 和不大于 的正整数 ,所有满足 的结点 的权值的异或和为 ;特殊地,若没有满足条件的结点 ,则需要满足 。
其中, 的值等于结点 和结点 之间的简单路径所包含的边的数量。特殊地,。
题目保证至少存在一组满足条件的数对 。
输入格式
本题有多组测试数据。
输入的第一行包含一个整数 ,表示测试数据组数。
接下来依次输入每组测试数据。对于每组测试数据:
- 第一行一个正整数 。
- 接下来 行,第 行包括 个整数,其中第 个整数表示 的值。
输出格式
对于每组测试数据,输出一行两个整数,分别表示你构造的数对 中 与 的值。
- 若你构造的数对 满足条件,则你可以获得该测试点 的分数;
- 否则,若你构造的数对 不满足条件,但存在一组满足条件的数对 满足 ,则你可以获得该测试点 的分数;
- 否则,若你构造的数对 不满足条件,但存在一组满足条件的数对 满足 ,则你可以获得该测试点 的分数;
- 否则,你不能获得该测试点的分数。
2
2
1 0
2 0
1 2
4
75 0 89 1 0 56
0 52 19 84 1 0
0 27 19 108 1 0
0 89 1 0 56 0
85 19 108 1 0 0
75 0 89 1 0 56
1 1 56 0 0 0
0 88 19 84 1 0
0 79 19 108 1 0
74 0 88 1 0 56
0 88 1 0 56 0
109 19 84 1 0 0
19 56 1 0 0 0
74 0 88 1 0 56
18 1 0 56 0 0
2 1
7 19
提示
【样例解释 #1】
对于第一组测试数据:
当构造的数对 时,存在一棵如图所示的二叉树符合题意,其中结点 的权值分别为 。
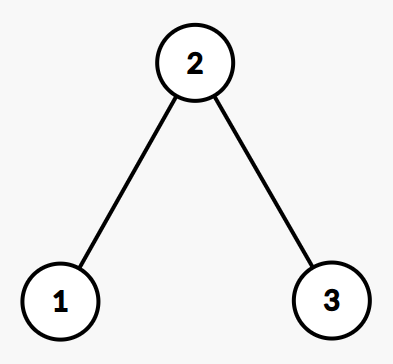
当你输出 2 2 时,你可以获得该测试点 的分数,因为 虽然不满足条件,但存在一组满足条件的数对 满足 。
当你输出 1 1 时,你也可以获得该测试点 的分数。
但当你输出 1 2 时,你将不能获得该测试点的分数。
【数据范围】
设 表示单个测试点中 的和。
对于所有测试数据,,,,,保证至少存在一组满足条件的数对 。
本题采用捆绑测试。
- Subtask 1(20 points):。
- Subtask 2(20 points):满足特殊性质。
- Subtask 3(60 points):无特殊限制。
特殊性质:存在一组数对 ,满足 ,,且在此基础上存在一棵符合题意的满二叉树,其所有结点的权值均为 。
