题目描述

题目译自 XXVIII Olimpiada Informatyczna – III etap Droga do domu

Bajtogród 的路网由 $n$ 个路口和 $m$ 条双向道路组成。每条道路连接两个不同的路口，且任意两个路口之间最多只有一条直接道路。道路可能经过隧道或高架桥。

路口 $1$ 附近有一所学校，Bajtek 每天在那里上学，而路口 $n$ 附近是他的家。早上，父母会开车送他去学校，但放学后他需要自己乘坐公共交通回家。今年公交车的时刻表又一次调整了。由于 Bajtogród 只提供单程票，每次上车都需要检票，Bajtek 决定制定一个最快的回家计划，且换乘次数不超过 $k$ 次。请你帮帮他！

每条公交线路的车辆都会按照固定的路线行驶，经过某些路口，并在每个路口停靠，供乘客上下车。同一线路的公交车会按照固定的时间间隔发车（具体细节见输入格式）。我们假设以下时间可以忽略不计：

• 公交车在路口的停靠时间；
• 从一辆公交车换乘到另一辆公交车的时间（假设无需等待）；
• 从学校走到路口 $1$ 以及从路口 $n$ 走回家的时间。

输入格式

输入的第一行包含五个整数 $n, m, s, k, t$ $(2 \leq n \leq 10000, 1 \leq m \leq 50000, 1 \leq s \leq 25000, 0 \leq k \leq 100, 0 \leq t \leq 10^{9})$，分别表示路口数量、道路数量、公交线路数量、Bajtek 最多允许的换乘次数，以及他离开学校的分钟数。路口编号从 $1$ 到 $n$。

接下来的 $m$ 行描述道路，每行包含三个整数 $a, b, c$ $(1 \leq a, b \leq n, a \neq b, 1 \leq c \leq 10^{9})$，表示编号为 $a$ 和 $b$ 的路口之间有一条双向道路，乘坐任何经过这条路的公交车通过它需要 $c$ 分钟。每对无序路口对 $\{a, b\}$ 在输入中最多出现一次。

接下来的 $2s$ 行描述公交线路，每条线路的描述占用两行。第一行包含三个整数 $\ell, x, y$ $(2 \leq \ell \leq n, 0 \leq x \leq 10^{9}, 1 \leq y \leq 10^{9})$，第二行包含 $\ell$ 个两两不同的整数 $v_{1}, v_{2}, \ldots, v_{\ell}$ $(1 \leq v_{i} \leq n)$。这表示该线路的公交车从路口 $v_{1}$ 在 $x + j \cdot y$ $(j = 0, 1, 2, \ldots)$ 分钟发车，然后依次经过路口 $v_{2}, v_{3}, \ldots, v_{\ell}$。保证对于 $1 \leq i < l$，路口 $v_i$ 和 $v_{i+1}$ 之间存在一条道路。

所有公交线路的 $\ell$ 之和不超过 $50000$。

输出格式

你的程序应输出一行，包含一个整数，表示 Bajtek 从学校离开后能到达家的最早分钟数。如果 Bajtek 无法在 $t$ 分钟后回家，则应输出 NIE。

4 4 2 1 1
1 2 2
2 3 4
1 3 3
4 3 2
4 0 10
1 2 3 4
3 2 7
1 3 2

8

下图展示了样例中的 Bajtogród 路网。圆圈表示路口，圆圈内的数字是路口编号；线条表示道路，线条旁的数字是经过该道路的行车时间。第 $1$ 条公交线路的路线用红色标记，第 $2$ 条公交线路的路线用蓝色标记。

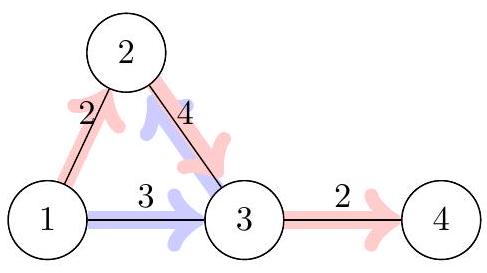
Bajtek 在 $t=1$ 分钟离开学校，在路口 $1$ 等待第 $2$ 条线路的公交车（第 $2$ 分钟到达），乘坐它到路口 $3$（第 $6$ 分钟到达），然后在路口 $3$ 换乘第 $1$ 条线路的公交车（第 $6$ 分钟到达路口 3），最终在第 $8$ 分钟到达家。

如果 $k=0$，Bajtek 必须在路口 $1$ 等待第 $1$ 条线路的公交车（第 $10$ 分钟发车），并在第 $18$ 分钟到达家。

样例 2

见附加文件下 [dro1.in](file:dro1.in) 和 [dro1.out](file:dro1.out)。

该样例满足 $n=10, m=45, k=10, t=123$，编号相邻的路口之间有长度为 $1$ 的道路，其他路口对之间有长度为 $100$ 的道路；公交车从 $0$ 分钟开始运行，每分钟都有车在相邻或相隔 $1$ 的路口之间运行，答案是 $132$；

样例 3

见附加文件下 [dro2.in](file:dro2.in) 和 [dro2.out](file:dro2.out)。

该样例满足 $n=103, m=102, k=100, t=0$，编号相邻的路口之间有长度为 $1$ 的道路，其他路口对之间没有直接道路；有一辆公交车在 $10^{9}$ 分钟发车，经过路口 $(1, 2, 3, \ldots, n)$，还有一些公交车从 $0$ 分钟开始运行，覆盖所有相邻路口对，答案是 $10^{9}+102$；

样例 4

见附加文件下 [dro3.in](file:dro3.in) 和 [dro3.out](file:dro3.out)。

该样例满足 $n=10000, m=17891, s=7891, k=50, t=0$，答案是 $11100000071$。

数据范围与提示

详细子任务附加限制及分值如下表所示。

子任务	附加限制	分值
$1$	$k=n$	$20$
$2$	每条公交线路：$v_{i} < v_{i+1}$	$20$
$3$	每条公交线路：$\ell=2$	$20$
$4$	$t=0$ 且每条公交线路：$x=0, y=1$	$20$
$5$	无附加限制	$20$