注意事项

在 LibreOJ 上，由于语言限制，目前只支持以下语言的提交：

• C++（标准为 C++ 17 及以上）

请在提交源代码前添加 #include "roadwork.h"。

题目描述

题目译自 2025년도 국제정보올림피아드 대표학생 선발고사 - 1차 선발고사 T3 「다리 보수 공사」

KOI 城市以一条横贯东西的大河为中心而建。河的北岸和南岸各分布着 $N$ 个村庄。北岸的村庄从下游向上游依次编号为 $A_{1}, A_{2}, \ldots, A_{N}$，南岸的村庄同样从下游向上游依次编号为 $B_{1}, B_{2}, \ldots, B_{N}$。因此，KOI 城市总共有 $2N$ 个村庄。

最初，KOI 城市的居民靠木筏往来交流，但随着现代化进程，他们开始修建跨越大河的桥梁。由于城市发展从下游开始，最早建成的桥梁连接了 $A_{1}$ 和 $B_{1}$，被居民称为 $0$ 号桥。随后，KOI 城市陆续修建了 $1$ 号桥、$2$ 号桥，乃至 $2N-2$ 号桥，总共建成 $2N-1$ 座桥梁。

从 $0$ 号桥开始，每座新桥都与前一座桥相邻修建。具体来说，对于任意 $0 \leq i \leq 2N-3$，若 $i$ 号桥连接 $A_{x}$ 和 $B_{y}$，则 $i+1$ 号桥要么连接 $A_{x}$ 和 $B_{y+1}$，要么连接 $A_{x+1}$ 和 $B_{y}$。这两种选择记录在一个长度为 $2N-2$ 的字符串 $S$ 中：若 $S[i] = \texttt{A}$，则 $i+1$ 号桥连接 $A_{x}$ 和 $B_{y+1}$；若 $S[i] = \texttt{B}$，则连接 $A_{x+1}$ 和 $B_{y}$。字符串 $S$ 中恰好有 $N-1$ 个 $\texttt{A}$ 和 $N-1$ 个 $\texttt{B}$。据此，可以证明以下事实：

• 不会出现连接不存在村庄的桥梁。
• 任意两个不同村庄之间总能通过桥梁往返。
• $2N-2$ 号桥必然连接 $A_{N}$ 和 $B_{N}$。

现在，KOI 城市计划对桥梁进行维修工程。维修将从 $2N-1$ 座桥梁中挑选若干座进行。由于施工会产生噪音，城市希望避免同一村庄连接的两座或更多桥梁同时维修。你的任务是帮助 KOI 城市在满足这一条件的前提下，尽可能多地维修桥梁，并计算出能修最多桥梁时的方案数，对 $10^{9}+7$ 取模后的余数。两个维修方案不同是指选中的桥梁集合不同。即使你只算出最多能修的桥梁数量，也能获得部分分数。

实现细节

你需要实现以下函数：

array<int, 2> roadwork(string S)

• $S$：长度为 $2N-2$ 的字符串。
• 该函数在一个测试用例中可能被调用 $T$ 次。
• 若最多能维修 $p$ 座桥梁，且维修 $p$ 座桥梁的方案数对 $10^{9}+7$ 取模后为 $q$，函数需返回 $[p, q]$，其中 $0 \leq q \leq 10^{9}+6$。

你提交的代码中不得包含任何输入输出函数。

样例 1

假设 $N=2$，$S=\texttt{AB}$，评测程序调用：

roadwork("AB")

下图展示了 KOI 城市的结构。

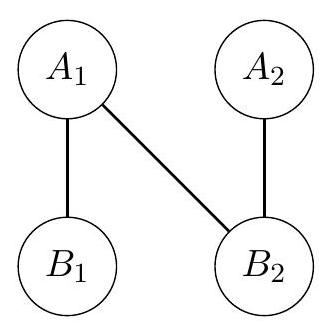
此时，$0$ 号桥连接 $A_{1}$ 和 $B_{1}$，$1$ 号桥连接 $A_{1}$ 和 $B_{2}$，$2$ 号桥连接 $A_{2}$ 和 $B_{2}$。选择 $0$ 号桥和 $2$ 号桥维修，可修最多 $2$ 座桥，且这种方案只有 $1$ 种。函数应返回 $[2,1]$。若返回 $[2,-1]$ 或 $[2,0]$ 等，仅正确返回数量，分数按部分计。

维修 $1$ 座桥有 $3$ 种方法，但这不是最多桥梁的情况，不予考虑。

样例 2

假设 $N=7$，$S=\texttt{AABBAABBAABB}$，评测程序调用：

roadwork("AABBAABBAABB")

下图展示了 KOI 城市的结构。

此时，最多可维修 $6$ 座桥，方案数有 $4$ 种。函数应返回 $[6,4]$。

数据范围与提示

对于所有输入数据，满足：

• $1 \leq T \leq 10$
• $2 \leq N \leq 2^{21}$
• $S$ 中恰好包含 $N-1$ 个 $\texttt{A}$ 和 $N-1$ 个 $\texttt{B}$。

详细子任务附加限制及分值如下表所示。

子任务	分值	附加限制
$1$	$4$	$N \leq 2^{1}$
$2$	$5$	$N \leq 2^{3}$
$3$	$6$	$N \leq 2^{5}$
$4$	$7$	$N \leq 2^{7}$
$5$	$8$	$N \leq 2^{9}$
$6$	$9$	$N \leq 2^{11}$
$7$	$10$	$N \leq 2^{13}$
$8$	$11$	$N \leq 2^{15}$
$9$	$12$	$N \leq 2^{17}$
$10$	$13$	$N \leq 2^{19}$
$11$	$15$	无附加限制

对于每个子任务，若仅正确返回最多桥梁数量，可获得 $40\%$ 的分数。

示例评测程序

示例评测程序接收以下格式的输入：

• 第 $1$ 行：$T$
• 第 $2+i$ $(0 \leq i \leq T-1)$ 行：$N\ S$

设第 $i+1$ 个测试用例中 roadwork 返回的数组为 $C[i]$，输出格式为：

• 第 $1+j$ $(0 \leq j \leq T-1)$ 行：$C[j][0]\ C[j][1]$

请注意，示例评测程序可能与实际评测程序有所不同。