loj#P4082. 「ROI 2023 Day2」山坡上的蜗牛
「ROI 2023 Day2」山坡上的蜗牛
题目描述
译自 ROI 2023 Day2 T1. Улитка на склоне
一只蜗牛悄悄地爬上了富士山的山顶,它想要下山。在山坡上有一些小路,形成了一个悬挂的二叉树。
树中有 个节点,用 条小路连接。山顶是树的根节点。在一些节点上,小路走到了尽头,它们是树的叶子节点。对于每个非叶子节点,都有两条小路向下延伸:一条向左,一条向右。
蜗牛想要从根节点开始沿着树下滑,直到到达一个叶子节点。它会沿着小路向下移动。在每个节点处,蜗牛可以选向左下滑或者向右下滑。蜗牛可以在根节点处选择任意一个方向开始下滑。在每个非根节点处,如果蜗牛选择的方向与前一个节点处的方向不同,那么它就会转弯。蜗牛不喜欢转弯,所以在从根节点到叶子节点的整个路径上,蜗牛最多愿意转弯 次。
给定树中节点的编号为 到 ,其中根节点的编号为 。给你 个查询。每个查询给出了一个节点 ,你需要求出如果蜗牛从根节点开始下滑最多转弯 次,并且在路径上经过节点 ,它能在多少个叶子节点处结束下滑。
输入格式
第一行包含三个整数 $n, k, q\ (3 \leq n \leq 2\times 10^5, 0 \leq k \leq n, 1 \leq q \leq 2\times 10^5)$,分别表示树中的节点数,蜗牛愿意转弯的最大次数,查询的数量。
接下来的 行中给出了树的形态。第 行包含一个整数 ,表示从第 个节点出发的小路的数量( 或 )。如果 ,那么在同一行中,接下来给出两个整数 ,分别表示从第 个节点出发的左边和右边的小路所通向的节点的编号。保证这个描述符合一个以第 个节点为根的悬挂二叉树。
接下来的 行中给出了查询。第 行包含一个整数 ,表示蜗牛在其路径上必须经过的节点的编号。
输出格式
对于每个查询,输出一行一个整数,表示如果蜗牛从根节点开始下滑最多转弯 次,并且在路径上经过节点 ,它能在多少个叶子节点处结束下滑。
7 1 4
2 2 4
0
2 6 5
2 3 7
0
0
0
1
4
3
5
3
2
1
0
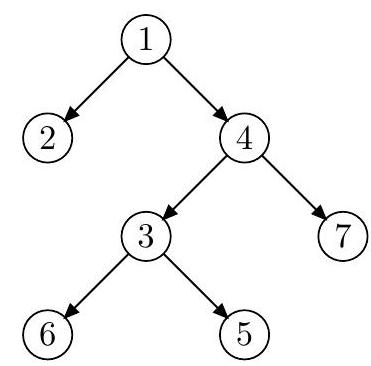
这是样例中的树的形态。
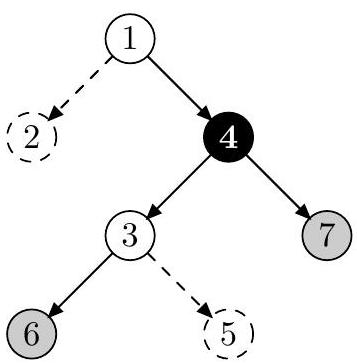
蜗牛必须经过 号节点,它能在 号节点处结束下滑。
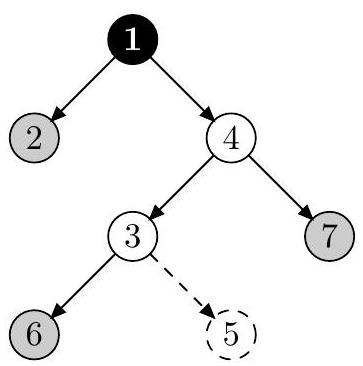
蜗牛必须经过 号节点,它能在 号节点处结束下滑。
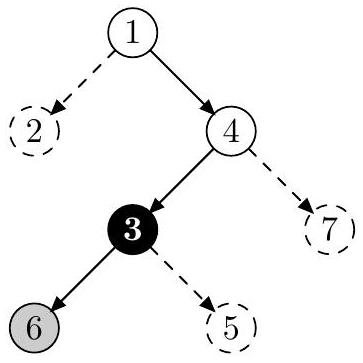
蜗牛必须经过 号节点,它能在 号节点处结束下滑。
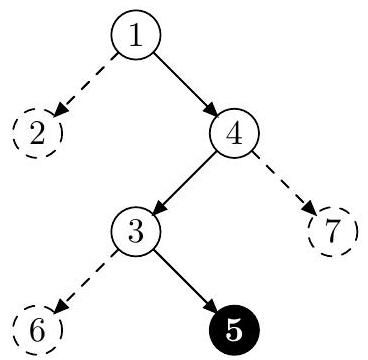
蜗牛必须经过 号节点,但是到达这个节点的路径已经包含了超过一个的转弯。因此,满足条件的叶子节点不存在。
数据范围与提示
详细子任务附加限制及分值如下表所示。其中子任务 是样例。
| 子任务编号 | 分值 | 附加限制 | 子任务依赖 |
|---|---|---|---|
| ;在所有查询中, 都是叶子节点 | |||
| 在所有查询中, 都是叶子节点 | |||
| 无附加限制 |
