题目描述

题目译自 eJOI2017 Problem D. Camel

让我们描述一种新的国际象棋棋子，并叫它「骆驼」。这种棋子横向和纵向可以越过两个格子，或斜向沿对角线方向越过一个格子。下图展示了一个骆驼放在中心的棋盘，标有 $\times$ 的位置是这个棋子能走到的位置。当然，棋子不能走到棋盘外。这里的棋盘是 $N\times N$ 大小的，本题中 $N$ 总能被 $5$ 整除。

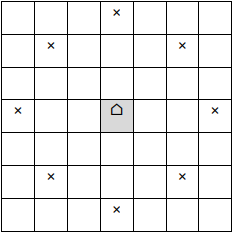
这个骆驼从棋盘的左上角出发。游戏要求这个棋子在棋盘上移动，并经过每个方格恰好一次。此外，在 $N^2-1$ 次移动后这个棋子再恰好移动一次就能回到出发点。这也就是所谓的「骆驼环」。

写一个程序找到一种游戏的进行方式，或者输出不存在这样的环。

输入格式

输入一个整数 $N$。

输出格式

输出如下内容：

• 如果你确定不存在这样的环，输出一行 NO。
• 否则输出 $N$ 行，每行包含 $N$ 个范围在 $1$ 到 $N^2$（包含两端）且互不相同的整数。第一行第一个数是 $1$。输出表示棋盘（$N\times N$ 的方格），其中的整数表示第几步走到这个格子中。请参考样例。

10

1 52 29 8 51 28 9 50 37 16
85 95 59 86 94 66 87 93 65 88
40 19 100 39 18 76 38 17 77 49
2 53 30 7 58 27 10 89 36 15
84 96 60 75 99 67 72 92 64 71
41 20 82 44 23 90 45 24 78 48
3 54 31 6 57 26 11 68 35 14
83 97 61 74 98 62 73 91 63 70
42 21 81 43 22 80 46 25 79 47
4 55 32 5 56 33 12 69 34 13

数据范围与提示

对于所有数据，$5\le N\le 10^3$，并保证 $N$ 可以被 $5$ 整除。

• 存在 $20$ 分的一组数据，保证 $N=5$；
• 其余 $16$ 组数据，每组数据 $5$ 分。