loj#P3551. 「COI 2020」Semafor
「COI 2020」Semafor
题目描述
你可能十分熟悉七段数码管,这是一种显示数码的器件,广泛使用于如手表或计算器等的数字设备上。由于它简单直观,并具有美感,这种设计被全球广泛接受。但小 Matej 仍然反对七段数码管的设计,并称只用五段数码管就可以更有效地获得与七段数码管同样的功能了。下图是五段数码管的设计图,每一段数码管用字母 到 编号。
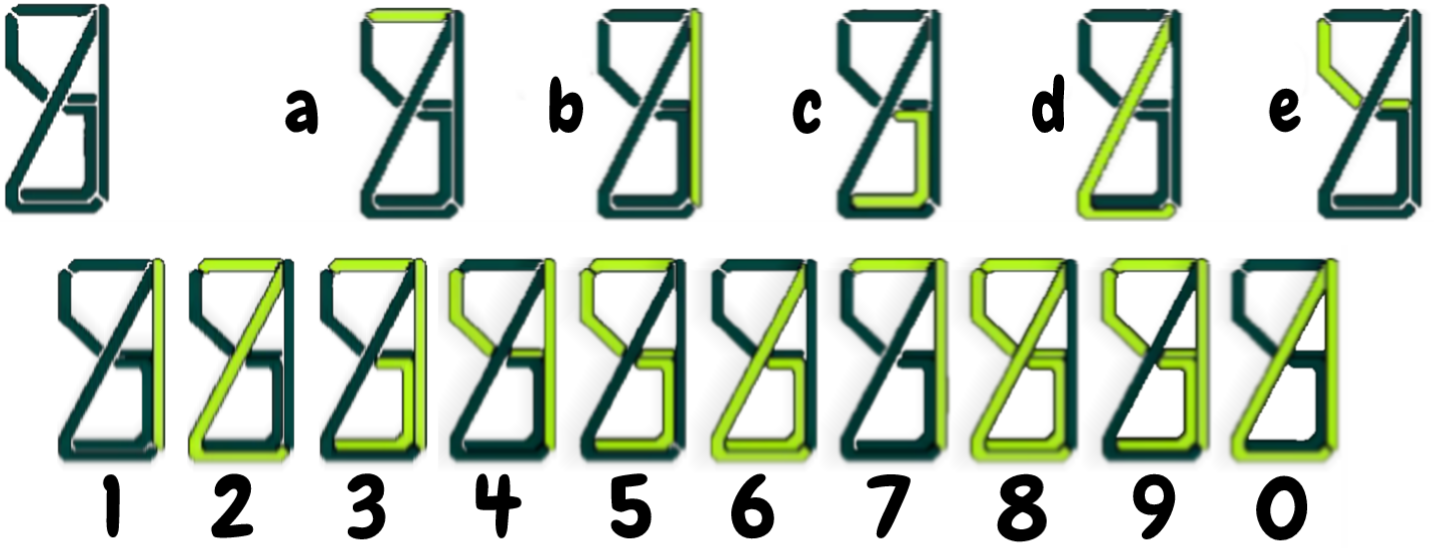
Matej 决定在克罗地亚经济最繁荣的分支——足球产业中迈出创业第一步。他革命性的设计将被运用在克罗地亚足球甲级联赛的电子换人牌上。他目前正在针对这个换人牌给克罗地亚足协主席做介绍。
这个换人牌由 个五段数码管组成,从左到右代表要离场的队员队服上编号的每一位。介绍刚开始时,换人牌上显示的数字是 ,之后 Matej 在每秒会进行以下操作中的一个:
- 点亮目前熄灭的某段数码管。
- 熄灭目前点亮的某段数码管。
Matej 总共会操作 步,并且他会保证在每 步操作之后,这个换人牌上会显示一个合法的数字。如果一个数字的每一位都像上面的图示一样正确显示(即,五段数码管显示的都是合法的数位),则称这个数字是合法的,具有前导零的数字也是合法的。
对于每一个最终状态(在 和 之间的整数),Matej 想知道有多少种不同的操作方式可以最后达到这种最终状态。当然,他需要遵守上面提到的所有限定。我们认为两个操作序列不同,当且仅当考虑在两个不同的换人牌上执行这两个序列,存在某一时刻两个换人牌显示的状态不同。
因为这个不同的操作方式数量可能会很大,你需要计算这个数量对 取模后的值。
输入格式
第一行四个整数 和 ,意义如题目描述。
输出格式
第 行输出有多少种不同的操作方式可以让最后的换人牌显示 。种类数对 取模后输出。
1 2 1 5
0
0
0
1
0
2
0
0
0
0
1 3 3 8
0
0
0
6
0
13
0
0
0
0
1 4 2 4
24
0
8
0
37
0
4
28
4
24
数据范围与提示
详细子任务附加限制与分值见下表。
| 子任务编号 | 附加限制 | 分值 |
|---|---|---|
